6.2余弦函数性质VIP免费

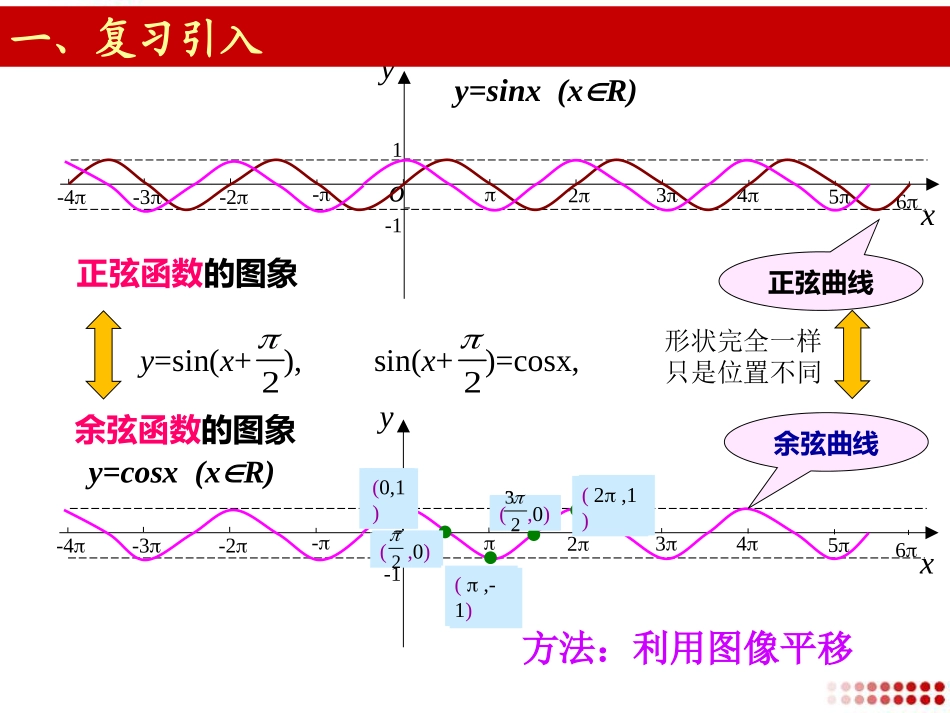
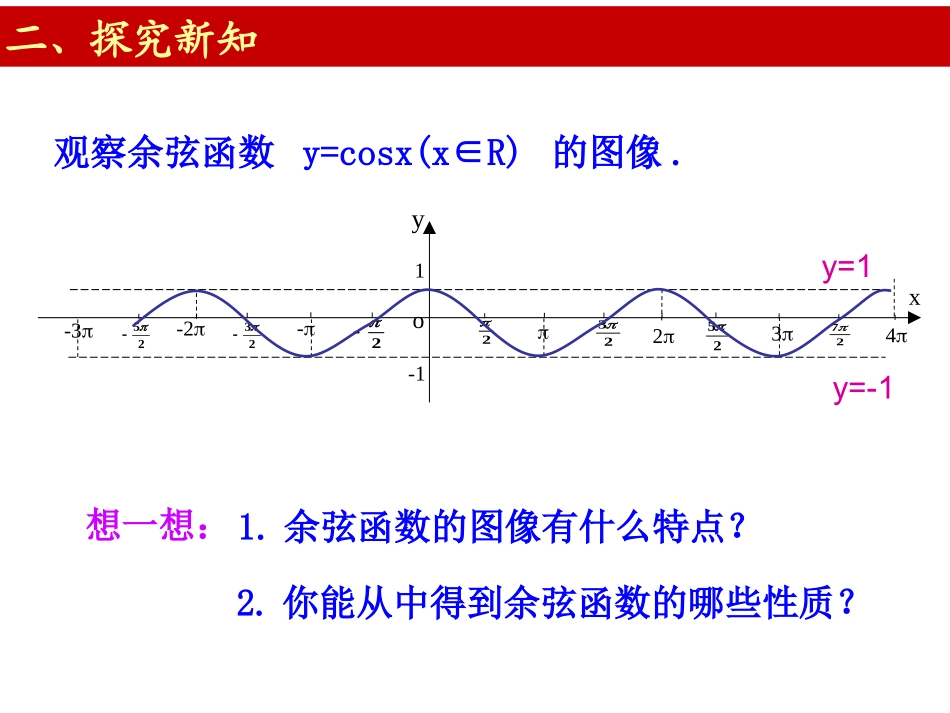
§1.6.2余弦函数的性质yxo--1234-2-31223252722325千阳中学闫倩x6yo--12345-2-3-41余弦函数的图象正弦函数的图象x6yo--12345-2-3-41y=sin(x+),2余弦曲线(0,1)(,0)2(,-1)(,0)23(2,1)正弦曲线形状完全一样只是位置不同(0,1)(,0)2(,-1)(,0)23(2,1)y=sinx(xR)y=cosx(xR)sin(x+)=cosx,2方法：利用图像平移一、复习引入二、探究新知观察余弦函数y=cosx(x∈R)的图像.想一想：2.你能从中得到余弦函数的哪些性质？1.余弦函数的图像有什么特点？yxo--1234-2-31223252722325y=1y=-1余弦函数的性质余弦函数的对称性对称中心：对称轴：)(,zkkx6o--12345-2-3-41yx)0,2(kzk例1画出函数的简图，根据图像讨论函数的性质．cos1yx=-xy=cosx00-1-2-10０－１０１解：列表1y=cosx-1y=cosx-1yxo--1234-2-31223252722325-2y=cosx函数y=cosx-1定义域值域奇偶性周期性单调性最值R[-2,0]偶函数2例2不求值，比较下列各对数值的大小23(1)cos()cos()34与45(2)cos()cos()78与3317(4)cos()cos()56与76(3)cos()cos()65与yxo--1234-2-31223252722325余弦函数的性质1.关于函数上的单调性，下列说法正确的是A.在上是减少的B.在上是增加的C.在上是减少的D.在上是减少的Acos,[0,2]yxx在[0,]23[,2]2[]2，3[,]22、函数y=1-2cosx的值域是________________3,13、函数y=1+cosx的对称中心是___________，对称轴是__________。Zkk),1,2(Zkkx,思考交流：x6yo--12345-2-3-41x6yo--12345-2-3-41四、课堂小结想一想：今天我们都学习了什么?余弦函数的基本性质定义域、值域、周期性、奇偶性、单调性、对称性yxo--1234-2-31223252722325四、课堂小结函数y=cosx定义域值域奇偶性周期性单调性最值R[-1,1]偶函数2谢谢！再见