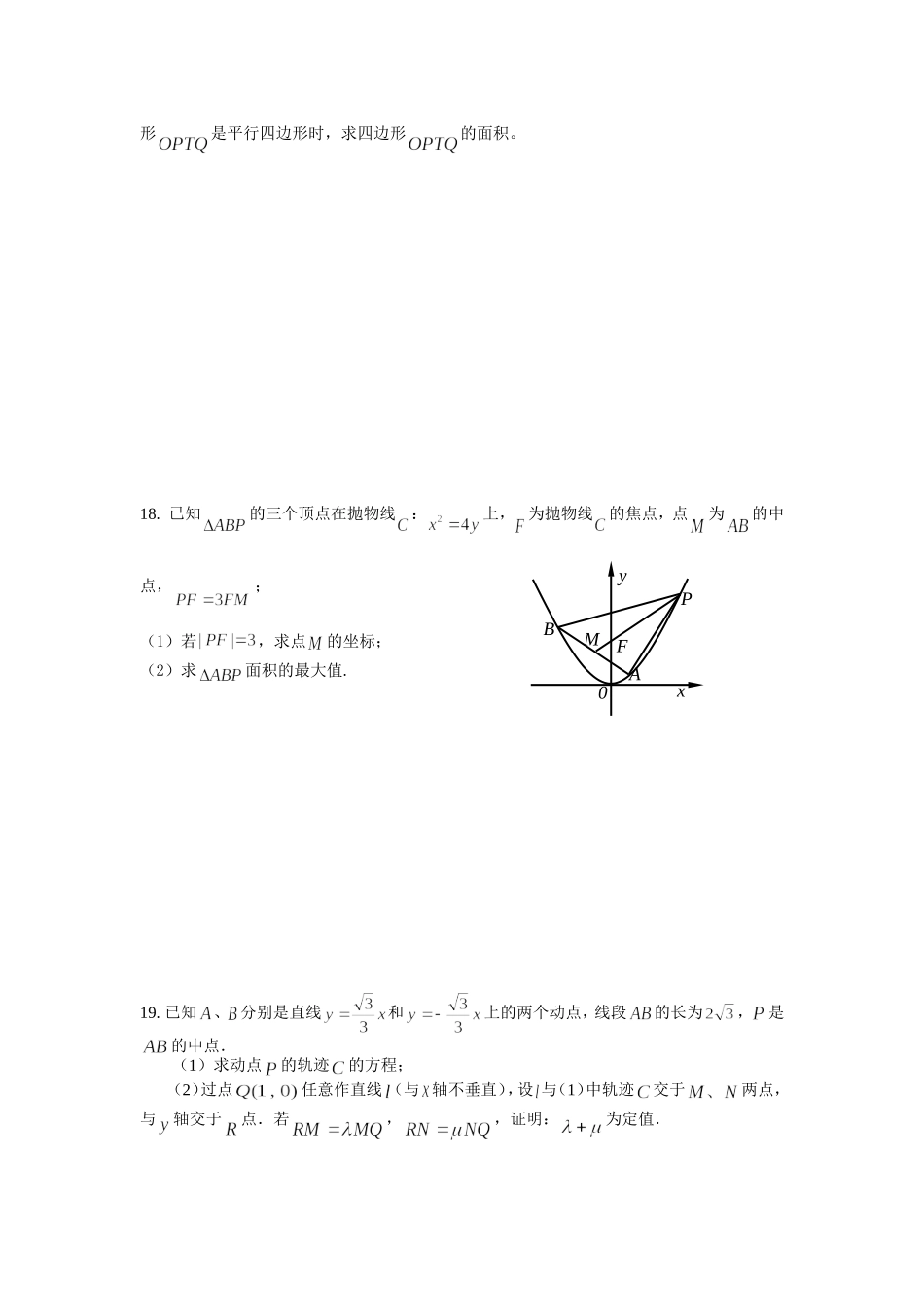
圆锥曲线单元练习二一.填空题(本题共70分,每题5分,请直接把答案填写在相应区域)1.离心率为的椭圆的标准方程为2.抛物线的焦点坐标为3.在平面直角坐标系中,双曲线中心在原点,焦点在轴上,一条渐近线方程为,则它的离心率为.4.若抛物线上两点到焦点的距离和是5,则线段中点到轴的距离为___________.5.已知双曲线的渐近线方程为焦点在轴上,焦点到相应渐进线的距离为2,则双曲线的方程为6.设点是椭圆上一点,是椭圆的两个焦点,则取最大值时点的坐标为7.在平面直角坐标系中,已知顶点顶点在椭圆上,则8.已知双曲线经过点且它的两条渐近线方程为那么双曲线的方程为9.已知动点在椭圆上,若点的坐标为(3,0),,且,则的最小值为___________________10.已知椭圆的离心率为过右焦点且斜率为的直线与椭圆相交与两点。若则11.等腰中,斜边,一个椭圆以为其中一个焦点,另一个焦点在线段上,且椭圆经过两点,则该椭圆的离心率为.12.已知正方形的坐标分别是,,,,动点M满足:,则.13.已知椭圆()与双曲线有公共的焦点,的一条渐近线与以的长轴为直径的圆相交于两点.若恰好将线段三等分,则=______.14.已知是椭圆长轴的两个端点,是椭圆上关于轴对称的两点,直线的斜率分别为,且的最小值为,则椭圆的离心率为二.解答题:(请写出相应的证明过程,文字说明或演算步骤)15.设椭圆C:的左焦点为F,上顶点为A,过点A与AF垂直的直线分别交椭圆C与轴正半轴于点P、Q,且.(1)求椭圆C的离心率;(2)若过A、Q、F三点的圆恰好与直线l:相切,求椭圆C的方程.16.已知中心在原点O,焦点在轴上的椭圆C的离心率为,点A、B分别是椭圆C的长轴、短轴的端点,点O到AB的距离为.(1)求椭圆C的标准方程;(2)已知点E(3,0),设点P、Q是椭圆C上的两个动点,满足EP⊥EQ,求的取值范围.17.已知椭圆:()的左焦点为,离心率为。(1)求椭圆的标准方程;(2)设为坐标原点,为直线上一点,过作的垂线交椭圆于,。当四边PBAMFyx0形是平行四边形时,求四边形的面积。18.已知的三个顶点在抛物线:上,为抛物线的焦点,点为的中点,;(1)若,求点的坐标;(2)求面积的最大值.19.已知、分别是直线和上的两个动点,线段的长为,是的中点.(1)求动点的轨迹的方程;(2)过点任意作直线(与轴不垂直),设与(1)中轨迹交于两点,与轴交于点.若,,证明:为定值.20.已知椭圆22220yxCabab:+=1>>的离心率为63,过右顶点A的直线与椭圆C相交于A、B两点,且(13)B,.(1)求椭圆C和直线的方程;(2)记曲线C在直线下方的部分与线段AB所围成的平面区域(含边界)为D.若曲线2222440xmxyym与D有公共点,试求实数m的最小值.一.填空题1.,2.,3.4.2,5.6.,7.8.9.10.11.12.13.14.二.解答题15.解(1)设椭圆C的焦距为2c,Q(x0,0),P(x1,y1),由F(-c,0),A(0,b)得. ,∴,即.又 ,∴,∴.又 点P在椭圆上,∴,整理得,又 ,∴,即,解得,故椭圆的离心率为.(2)由(1)知,,故,于是Q()、F(),△AQF的外接圆圆心为(),半径. △AQF的外接圆与直线相切,∴,解得a=2,∴,故椭圆C的方程为.16.17.(1)由已知得:,,所以又由,解得,所以椭圆的标准方程为:.(2)设T点的坐标为,则直线TF的斜率.当时,直线PQ的斜率,直线PQ的方程是当时,直线PQ的方程是,也符合的形式.将代入椭圆方程得:.其判别式.设,则.因为四边形OPTQ是平行四边形,所以,即.所以解得.此时四边形OPTQ的面积.18.(1)由题意知,焦点为,准线方程为,设,由抛物线的定义知,,得到,代入求得或,所以或,由得或,(2)设直线的方程为,,,,由得,于是,所以,,所以的中点的坐标,由,所以,所以,因为,所以,由,,所以,又因为,点到直线的距离为,所以,记,,令解得,,所以在上是增函数,在上是减函数,在上是增函数,又,所以当时,取得最大值,此时,所以的面积的最大值为.19.(1)设,,. 是线段的中点,∴ 分别是直线和上的点,∴和.∴又,∴.∴,∴动点的轨迹的方程为.(2)依题意,直线的斜率存在,故可设直线的方程为.设、、,则两点坐标满足方程组消去并整理,得...