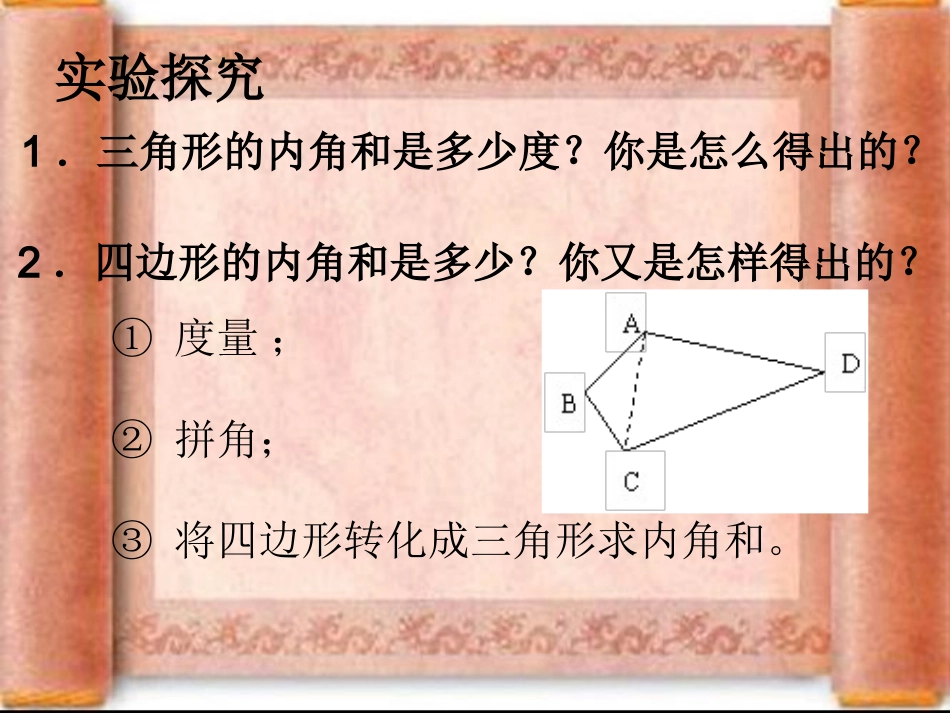
第六章平行四边形第六章平行四边形44多边形的内角和与外角和((一一))授课人:陈琳创设现实情境,提出问题1.三角形是如何定义的?2.仿照三角形定义,你能学着给四边形、五边形……边形下定义吗?实验探究1.三角形的内角和是多少度?你是怎么得出的?2.四边形的内角和是多少?你又是怎样得出的?①度量;②拼角;③将四边形转化成三角形求内角和。•使∠C(即图1⑵中∠1)的位置不动,先把∠B向右平移到∠2位置,再把∠A绕某个点旋转到∠3的位置,这3个角恰好组成了1个平角.123图1图3⑴⑵A1BCD234CABDFE124⑶3先把任意四边形ABCD4个内角撕开(如图3⑴),然后保持∠C不动(如图3⑵中的∠1),把∠A平移到∠2的位置,再分别把∠B、∠D绕某点旋转到∠3、∠4的位置,我发现这4个角恰好拼成1个周角.用拼角验证多边形内角和公式3.在四边形内角和的探索过程中,用到了几种方法,你认为哪种方法好?请讲述你的理由。4.根据四边形的内角和的求法,你能否求出五边形的内角和呢?六边形,七边形呢?方法总结:结论:从多边形的一个顶点可以引出(n-3)条对角线,把n边形分成(n-2)个三角形。从而得出:n边形的内角和是(n-2)·180°。例题讲解例1.一个多边形的内角和为1440°,则它是几边形?解:由题意知,(n-2)×1800=14400解得:n=10所以它是10边形。例题讲解•例2:已知一个多边形的边数增加一倍后,内角和增加19800,求原多边形的边数。设原多边形边数为n,则增加后的边数为2n根据题意得,(2n-2)×1800-(n-2)×1800=19800解得,n=11答:原多边形是11边形拓展延伸想一想:观察图中的多边形,它们的边、角有什么特点?正多边形定义:在平面内,每个内角都相等、每条边也都相等的多边形叫做正多边形。议一议:①一个多边形的边都相等,它的内角一定都相等吗?②一个多边形的内角都相等,它的边一定都相等吗?练一练:①正三角形、正四边形(正方形)、正五边形、正六边形、正八边形的内角分别是多少度?②正n边形的内角是多少度?③一个正多边形的每个内角都是150°,求它的边数?思维升华议一议:剪掉一张长方形纸片的一个角后,纸片还剩几个角?这个多边形的内角和是多少度?与同伴交流.知识小结1.过本节课的学习,你学到了哪些知识?有何体会?2.在学习多边形的有关概念时,我们使用了由特殊到一般的数学方法,并运用了类比、转化的思想方法。作业:作业:155页习题6.71,2题;