双曲线的参数方程VIP免费

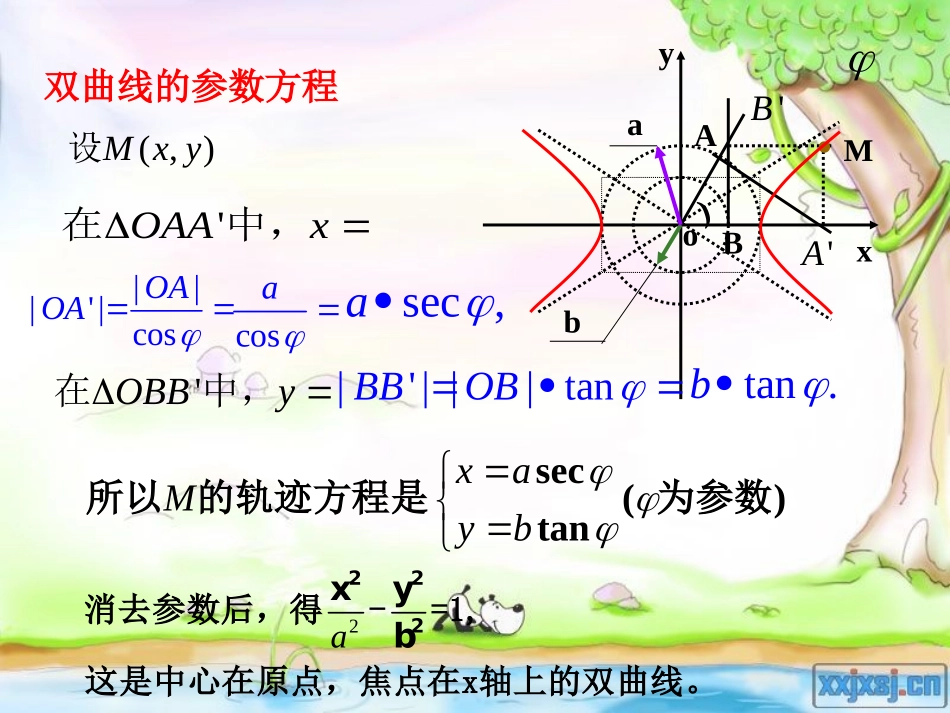
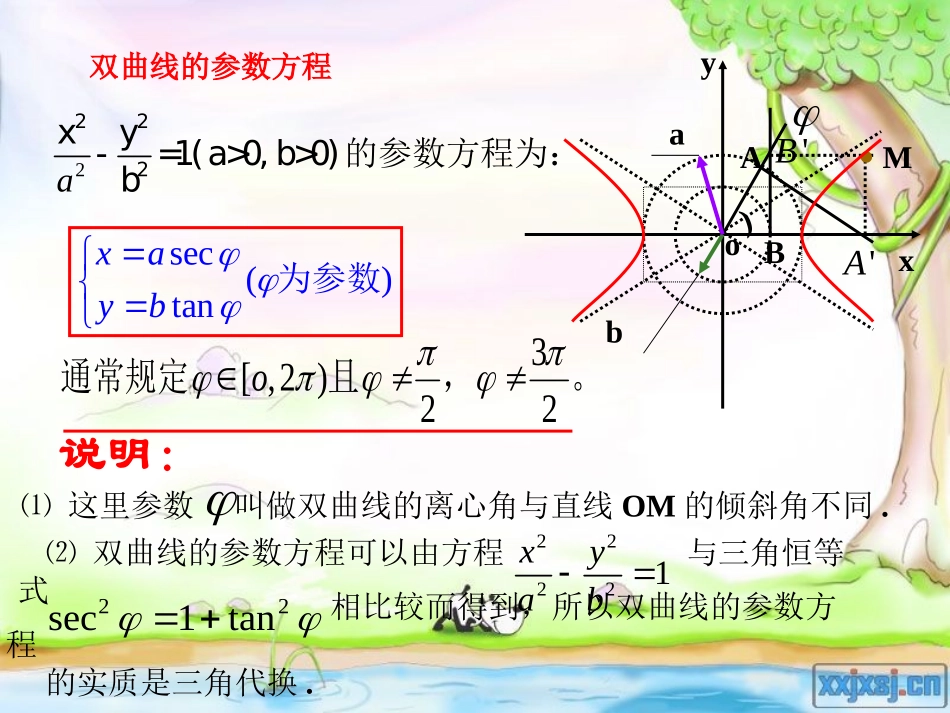
二、圆锥曲线的参数方程2、双曲线的参数方程•baoxy)MBA'B'A'OBBy在中，(,)Mxy设|'|||tanBBOBtan.b'OAAx在中，|||'|cosOAOAcosasec,asec()tanxaMyb所以的轨迹方程是为参数2a222xy消去参数后，得-=1,b这是中心在原点，焦点在x轴上的双曲线。双曲线的参数方程双曲线的参数方程•baoxy)MBA'B'Asec()tanxayb为参数2a222xy-=1(a>0,b>0)的参数方程为：b3[,2)22o通常规定且，。⑵双曲线的参数方程可以由方程与三角恒等式22221xyab22sec1tan相比较而得到，所以双曲线的参数方程的实质是三角代换.说明：⑴这里参数叫做双曲线的离心角与直线OM的倾斜角不同.例2、2222100xyMabOabMABMAOB(,)如图，设为双曲线任意一点，为原点，过点作双曲线两渐近线的平行线，分别与两渐近线交于，两点。探求平行四边形的面积，由此可以发现什么结论？OBMAxy.byxa双曲线的渐近线方程为：解：tan(sec).MbybxaaA不妨设M为双曲线右支上一点，其坐标为,则直线的方程为（asec,btan）：①b将y=x代入①，解得点A的横坐标为aAax=（sectan）2.Bax=（se同理可得，点B的横坐cta2标n为）.ba设AOx=,则tan.MAOB所以的面积为MAOBS=|OA||OB|sin2=ABxxsin2coscos2222a(sec-tan)=sin24costan.2baba22aa=22MAOB由此可见，平行四边形的面积恒为定值，与点M在双曲线上的位置无关。