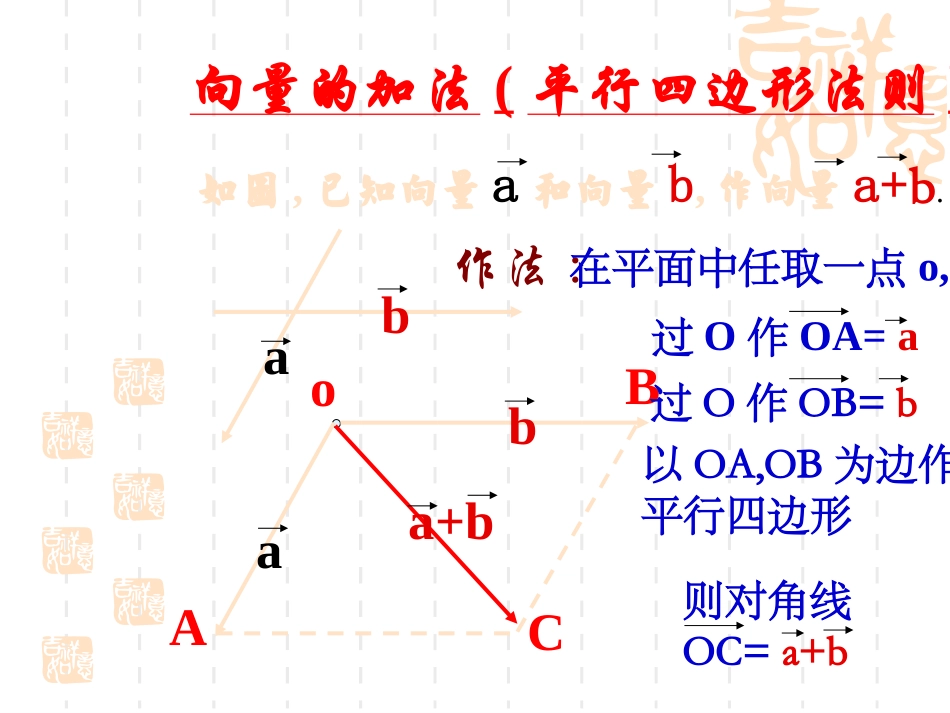
向量的加法(三角形法则)如图,已知向量a和向量b,作向量a+b.ab作法:在平面中任取一点o,o则OB=a+b.过A作AB=b过O作OA=aa+baAbBa向量的加法(平行四边形法则)如图,已知向量a和向量b,作向量a+b.作法:在平面中任取一点o,ob以OA,OB为边作平行四边形CaAbBa+b则对角线OC=a+b过O作OB=b过O作OA=a向量的减法(三角形法则)如图,已知向量a和向量b,作向量a-b.ab作法:在平面中任取一点o,oaAbBa-b过O作OB=b过O作OA=a则BA=a-b试作出:试作出:aa++aa++aa和和(-(-aa)+(-)+(-aa)+(-)+(-aa))已知非零向量已知非零向量aa(如(如图)图)aaaaaaaa-a-a-a-a-a-aOOAABBCCPPQQMMNN相同向量相加以后,相同向量相加以后,和的长度与方向有什么变化?和的长度与方向有什么变化?aaOOAABBCC3a3a一般地,一般地,实数实数λλ与向量与向量aa的的积积是一个是一个向量向量,记,记作作λλaa,它的长度和方向规定如下:,它的长度和方向规定如下:(1)|λ(1)|λaa|=|λ|||=|λ||aa||(2)(2)当当λ>0λ>0时时,λ,λaa的方向与的方向与aa方向相同;方向相同;当当λ<0λ<0时时,λ,λaa的方向与的方向与aa方向相反;方向相反;特别地,当特别地,当λ=0λ=0或或a=a=00时时,λ,λaa==00设设a,ba,b为任意向量,为任意向量,λ,μλ,μ为任意实数,则为任意实数,则有:①有:①λ(μλ(μaa)=(λμ))=(λμ)aa②②((λ+μλ+μ))a=a=λλa+a+μμaa③③λ(λ(a+ba+b)=λ)=λa+a+λλbb答案答案::-1-122aa55bb-a+-a+55bb--22cc例例11计算:计算:(1)((1)(--3)×43)×4aa(2)3((2)3(a+ba+b))–2(–2(a-ba-b))-a-a(3)(2(3)(2aa+3+3b-cb-c))–(3–(3a-a-22bb++cc))特别地,(-λ)a=a=--((λa)=λ(-a),λ(a-b)=λa-λb.b例:如图:ABCD的两条对角线交于点M,且,试求bADaAB,.,,,MDMCMBMAADBMCa对于向量对于向量a(a≠0),ba(a≠0),b,以,以及实数及实数λλ。。问题问题11:如果:如果b=b=λλa,a,那么,向量那么,向量aa与与bb是否共是否共线?线?问题问题22:如果:如果向量向量aa与与bb共线共线那么,那么,b=b=λλaa??如果向量如果向量bb与非零向量与非零向量aa共线共线,,那么那么有且只有一个实数有且只有一个实数λλ,使得,使得b=b=λλaa..例如图,已知任意两个非零向量a,b,试作OA=a+b,OB=a+2b,OC=a+3b.判断A、B、C三点之间的位置关系,并说明理由.ab设,是两个不共线向量,已知=2+k,=+3,=2,若三点A,B,D共线,求k的值。1e2eABCBCD1e2e1e2e1e2e变式:ABCOa2b3bb如图,在平行四边形如图,在平行四边形ABCDABCD中,点中,点MM是是ABAB中点,中点,点点NN在线段在线段BDBD上,且有上,且有BN=BDBN=BD,求证:,求证:MM、、NN、、CC三点共线。三点共线。31ADBCMN小结回顾小结回顾二、定理的应用:二、定理的应用:1.1.证明向量共线证明向量共线2.2.证明三点共线证明三点共线:AB=:AB=λλBCA,B,CBCA,B,C三点共线三点共线3.3.证明两直线平行证明两直线平行::AB=AB=λλCDABCD∥CDABCD∥ABAB与与CDCD不在同一直线上不在同一直线上直线直线AB∥AB∥直线直线CDCD一、一、①①λλaa的定义及运算律的定义及运算律②②向量共线定理向量共线定理(a≠0)(a≠0)b=b=λλaa向量向量aa与与bb共线共线练习:P1001、2、3、4、5、6课本课本::PP101101第第99题题,,第第1010题题,,第第1212题题BB组第组第33题题选作选作::以点以点OO为起点为起点的三个向量的三个向量a,b,ca,b,c的终点分的终点分别为别为A,B,C,A,B,C,如图如图,,若若c=α·a+β·b,c=α·a+β·b,且实数且实数α+β=1,α+β=1,求证求证:A,B,C:A,B,C三点共三点共线线abcABC