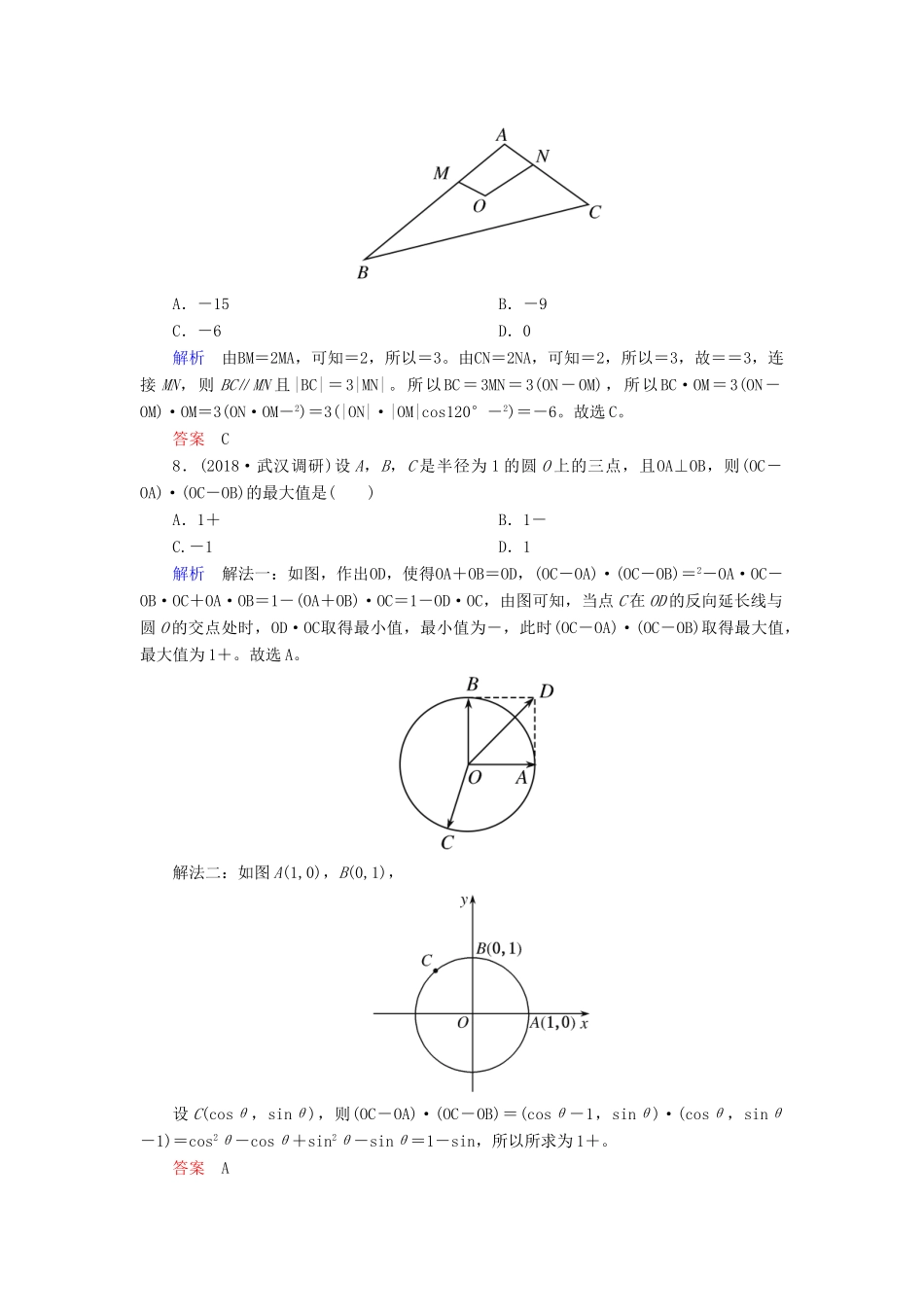
小题专练·作业(二)平面向量、复数1.(2018·全国卷Ⅰ)设z=+2i,则|z|=()A.0B.C.1D.解析解法一:因为z=+2i=+2i=+2i=i,所以|z|==1。故选C。解法二:因为z=+2i==,所以|z|=||===1,故选C。答案C2.(2018·福州联考)如果复数z=,则()A.z的共轭复数为1+iB.z的实部为1C.|z|=2D.z的实部为-1解析因为z====-1-i,所以z的实部为-1,故选D。答案D3.(2018·福建质检)庄严美丽的国旗和国徽上的五角星是革命和光明的象征。正五角星是一个非常优美的几何图形,且与黄金分割有着密切的联系:在如图所示的正五角星中,以A,B,C,D,E为顶点的多边形为正五边形,且=。下列关系中正确的是()A.BP-TS=RSB.CQ+TP=TSC.ES-AP=BQD.AT+BQ=CR解析结合题目中的图形可知BP-TS=TE-TS=SE=RS=RS。故选A。答案A4.(2018·贵阳摸底)如图,在边长为1的正方形组成的网格中,平行四边形ABCD的顶点D被阴影遮住,找出D点的位置,AB·AD的值为()A.10B.11,C.12D.13解析以点A为坐标原点,建立如图所示的平面直角坐标系,A(0,0),B(4,1),C(6,4),根据四边形ABCD为平行四边形,可以得到D(2,3),所以AB·AD=(4,1)·(2,3)=8+3=11。故选B。答案B5.(2018·武汉调研)已知复数z满足z+|z|=3+i,则z=()A.1-iB.1+iC.-iD.+i解析设z=a+bi,其中a,b∈R,由z+|z|=3+i,得a+bi+=3+i,由复数相等可得解得故z=+i。故选D。答案D6.(2018·南宁摸底)已知O是△ABC内一点,OA+OB+OC=0,AB·AC=2且∠BAC=60°,则△OBC的面积为()A.B.C.D.解析因为OA+OB+OC=0,所以O是△ABC的重心,于是S△OBC=S△ABC。因为AB·AC=2,所以|AB|·|AC|·cos∠BAC=2,因为∠BAC=60°,所以|AB|·|AC|=4。又S△ABC=|AB|·|AC|sin∠BAC=,所以△OBC的面积为。故选A。答案A7.(2018·天津高考)在如图的平面图形中,已知OM=1,ON=2,∠MON=120°,BM=2MA,CN=2NA,则BC·OM的值为()A.-15B.-9C.-6D.0解析由BM=2MA,可知=2,所以=3。由CN=2NA,可知=2,所以=3,故==3,连接MN,则BC∥MN且|BC|=3|MN|。所以BC=3MN=3(ON-OM),所以BC·OM=3(ON-OM)·OM=3(ON·OM-2)=3(|ON|·|OM|cos120°-2)=-6。故选C。答案C8.(2018·武汉调研)设A,B,C是半径为1的圆O上的三点,且OA⊥OB,则(OC-OA)·(OC-OB)的最大值是()A.1+B.1-C.-1D.1解析解法一:如图,作出OD,使得OA+OB=OD,(OC-OA)·(OC-OB)=2-OA·OC-OB·OC+OA·OB=1-(OA+OB)·OC=1-OD·OC,由图可知,当点C在OD的反向延长线与圆O的交点处时,OD·OC取得最小值,最小值为-,此时(OC-OA)·(OC-OB)取得最大值,最大值为1+。故选A。解法二:如图A(1,0),B(0,1),设C(cosθ,sinθ),则(OC-OA)·(OC-OB)=(cosθ-1,sinθ)·(cosθ,sinθ-1)=cos2θ-cosθ+sin2θ-sinθ=1-sin,所以所求为1+。答案A9.(2018·天津高考)i是虚数单位,复数=______。解析===4-i。答案4-i10.(2018·江苏高考)若复数z满足i·z=1+2i,其中i是虚数单位,则z的实部为________。解析复数z==(1+2i)(-i)=2-i的实部是2。答案211.(2018·合肥质检)已知平面向量a,b满足|a|=1,|b|=2,|a+b|=,则a在b方向上的投影等于______。解析解法一:因为|a|=1,|b|=2,|a+b|=,所以(a+b)2=|a|2+|b|2+2a·b=5+2a·b=3,所以a·b=-1,所以a在b方向上的投影为=-。解法二:记a=OA,a+b=OB,b=AB,由题意知|OA|=1,|OB|=,|AB|=2,则2+2=2,△AOB是直角三角形,且∠OAB=,所以a在b方向上的投影为|OA|cos=1×=-。答案-12.(2018·惠州调研)在四边形ABCD中,AB=DC,P为CD上一点,已知|AB|=8,|AD|=5,AB与AD的夹角为θ,且cosθ=,CP=3PD,则AP·BP=______。解析因为AB=DC,CP=3PD,所以AP=AD+DP=AD+AB,BP=BC+CP=AD-AB,又|AB|=8,|AD|=5,cosθ=,所以AD·AB=8×5×=22,所以AP·BP=·=2-AD·AB-2=52-11-×82=2。答案213.(2018·广东二模)如图,半径为1的扇形AOB中,∠AOB=,P是弧AB上的一点,且满足OP⊥OB,M,N分别是线段OA,OB...