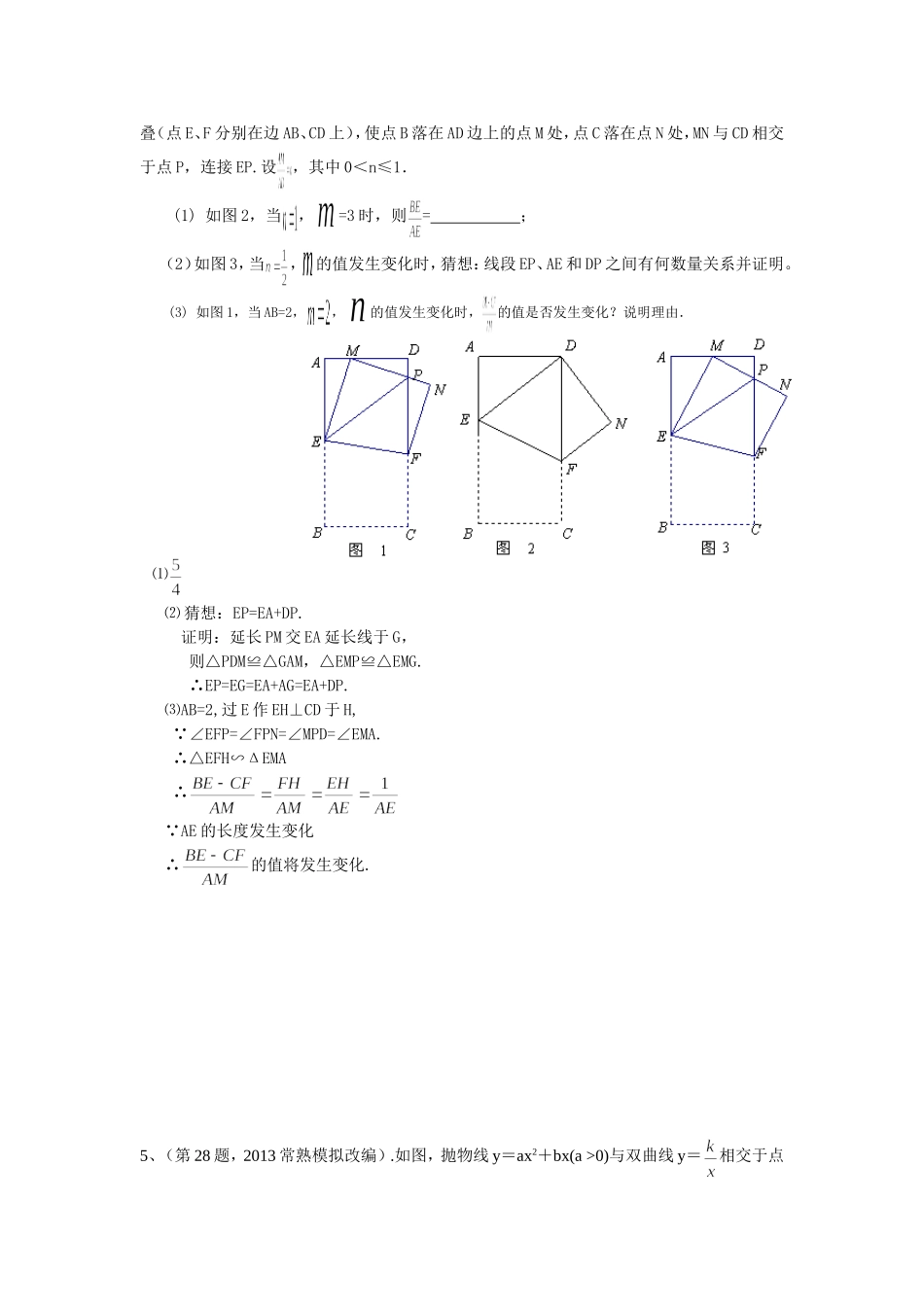
2013一模分析会交流(搬经镇中)1、(选择第10题)(2013海安一模改编)如图,BC=,A=,已知Rt△ABC,D1是斜边AB的中点,过D1作D1E1⊥AC于E1,连接BE1交CD1于D2;过D2作D2E2⊥AC于E2,连接BE2交CD1于D3;过D3作D3E3⊥AC于E3,…,如此继续,可以依次得到点E4、E5、…、E2013则CE2013的大小为()A.BCD答:C分析:先由勾股定理得出AC=6后再利用A字型和X型相似得出:CE1=CE2=CE3=CE4=......CE2013==2、(填空第18题,2013年常熟一模改编)如图,⊙O是以原点为圆心,2为半径的圆,点P是直线y=-x+6上的一点,过点P作⊙O的一条切线PQ,Q为切点,则△OPQ面积最小值为答:分析:在Rt△OPQ中,,△OPQ的面积最小即PQ长度最小时,PO最小为时,PQ为4,面积最小为3、(第27题,2013武汉模拟改编)如图1,在矩形纸片ABCD中,,其中≥1,将它沿EF折叠(点E、F分别在边AB、CD上),使点B落在AD边上的点M处,点C落在点N处,MN与CD相交于点P,连接EP.设,其中0<n≤1.(1)如图2,当,=3时,则=;(2)如图3,当,的值发生变化时,猜想:线段EP、AE和DP之间有何数量关系并证明。(3)如图1,当AB=2,,的值发生变化时,的值是否发生变化?说明理由.⑴⑵猜想:EP=EA+DP.证明:延长PM交EA延长线于G,则△PDM≌△GAM,△EMP≌△EMG.∴EP=EG=EA+AG=EA+DP.⑶AB=2,过E作EH⊥CD于H,∵∠EFP=∠FPN=∠MPD=∠EMA.∴△EFH∽ΔEMA∴∵AE的长度发生变化∴的值将发生变化.5、(第28题,2013常熟模拟改编).如图,抛物线y=ax2+bx(a>0)与双曲线y=相交于点A,B.已知点A的坐标为(1,4),点B在第三象限内,连结AB交y轴于点E,且S△BOE=S△AOB(O为坐标原点).(1)点B的坐标;(2)过点A作直线平行于x轴交抛物线于另一点C.问在y轴上是否存在点P,使△POC与△OBE相似,若存在,求出点P的坐标;若不存在,请简要说明理由;(3)抛物线与x轴的负半轴交于点D,过点B作直线l∥OC轴,点Q在直线l上运动,且点Q的横坐标为t,试探索:当S△AOB-2时,综上所述,