天津市六校高三数学第三次模拟联考试卷 理新人教A版试卷VIP免费

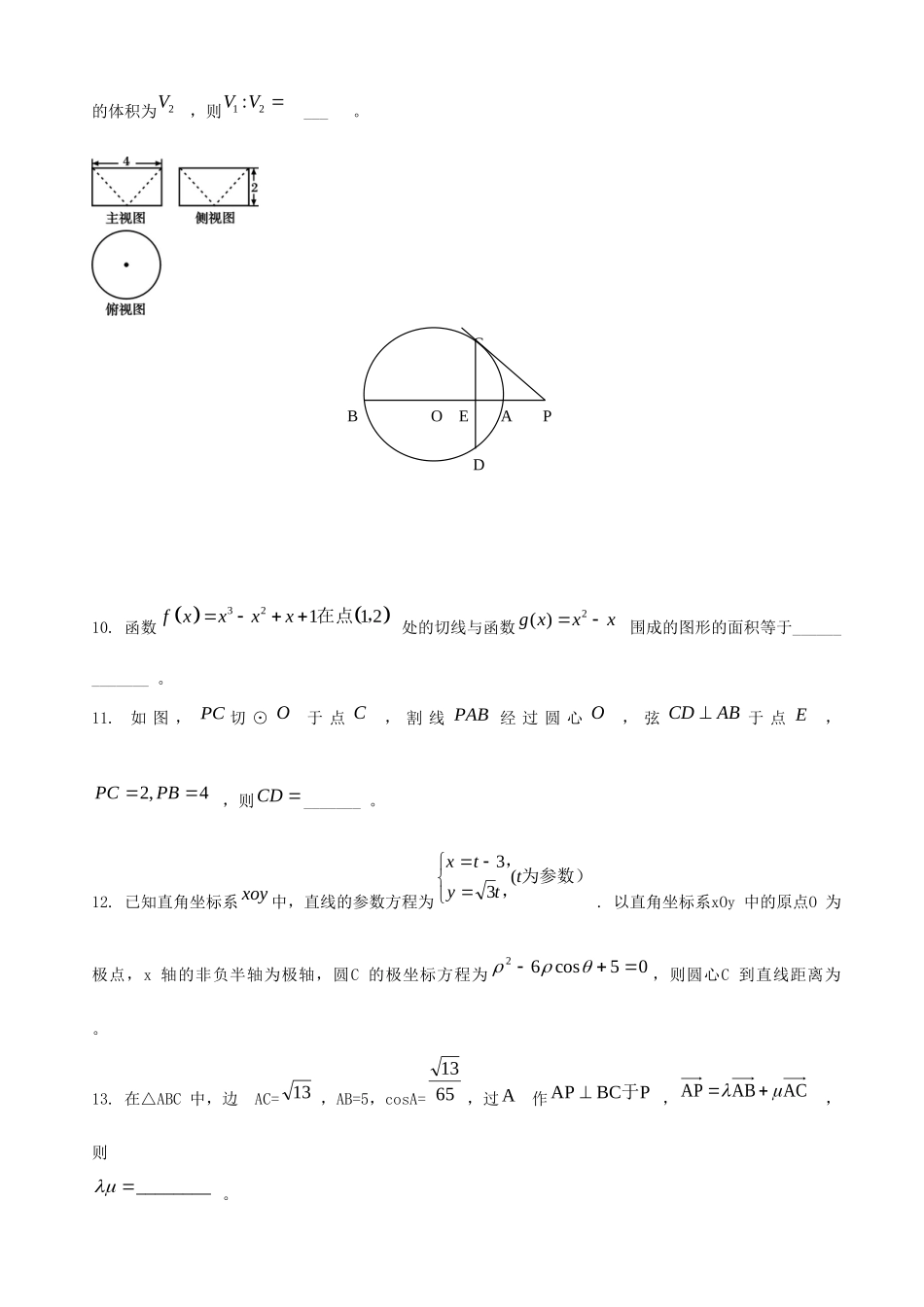
天津市六校2014届高三数学第三次模拟联考试题理（无答案）新人教A版本试卷分第Ⅰ卷（选择题）和第Ⅱ卷，共4页满分150分.考试时间120分钟.，将I卷答案填涂在，答题卡上，将第II卷答案填写在答题纸上，答在试卷上无效。一、选择题：（本大题共6小题，每小题5分，共30分。）1.若复数i12ia是纯虚数，其中i是虚数单位，则实数a的值为（）A.15B.2C.12D.252.设x、y满足22142yxyxyx，则yxz（）A．有最小值2,无最大值B．有最小值2,最大值3C．有最大值3,无最大值D．既无最小值,也无最大值3.已知函数sin()yAxk的最大值为4，最小值为0，最小正周期为，直线3x是其图像的一条对称轴，则下面各式中符合条件的解析式为（）A．4sin(4)6yxB．2)62sin(2xy否开始结束?输出是C．2sin(4)23yxD．2)62sin(2xy4.执行如图所示的程序框图．若输出31s，则框图中?处可以填入()A.B.C.D.5.在38(1)(1)xx的展开式中,含2x项的系数是n，若0122(8)nnnnxaaxaxax，则12naaa()A.1B.-1C.1-78D.-1+786.已知函数1,021,0.xxxfxx，若关于x的方程20fxxk有且只有一个的实根，则实数k的取值范围为（）[A.1,2B.)2(]1(C.0,1D.1,7.双曲线22221(0,0)xyabab的左、右焦点分别为F1,F2,渐近线分别为12,ll,点P在第一象限内且在1l上,若2l⊥PF1,2l//PF2,则双曲线的离心率（）A．5B．2C．3D．28.设*{1,2,3}()nXnnN，对nX的任意非空子集A，定义()fA为A中的最大元素，当A取遍nX的所有非空子集时，对应的()fA的和为nS，则5S（）[来A.104B.120C.124D.129二、填空题：（本大题共6小题，每小题5分，共30分。）9.已知某几何体的三视图如图所示，其中俯视图中圆的直径为4，该几何体的体积为1V,直径为2的球的体积为2V，则12:VV___。10.函数32112fxxxx在点，处的切线与函数xxxg2)(围成的图形的面积等于_____________。11.如图，PC切⊙O于点C，割线PAB经过圆心O，弦CDAB于点E，4,2PBPC，则CD_______。12.已知直角坐标系xoy中，直线的参数方程为为参数），，ttytx(33.以直角坐标系xOy中的原点O为极点，x轴的非负半轴为极轴，圆C的极坐标方程为05cos62，则圆心C到直线距离为。13.在△ABC中，边AC=13，AB=5，cosA=6513，过A作PBCAP于，ACABAP，则________。PDCBAOE14.已知()2xfx()xR可以表示为一个奇函数()gx与一个偶函数()hx之和，若不等式()()20agxhx对于]3,2[x恒成立，则实数a的取值范围是________。三、解答题：本大题共6小题，共80分．解答应写出文字说明、证明过程或演算步骤．15．已知函数wxwxwxxf2213coscossin)(，,0wxR且函数()fx的最小正周期为.(1)求w的值和函数()fx的单调增区间；(2)在ABC中，角A、B、C所对的边分别是a、b、c，又4()235Af，1b，ABC的面积等于3，求边长a的值．16．由于当前学生课业负担较重，造成青少年视力普遍下降，现从湖口中学随机抽取16名学生，经校医用对数视力表检查得到每个学生的视力状况的茎叶图(以小数点前的一位数字为茎，小数点后的一位数字为叶)如下：（1）指出这组数据的众数和中位数；（2）若视力测试结果不低于5.0，则称为“goodsight”，求校医从这16人中随机选取3人，至多有2人是“goodsight”的概率；（3）以这16人的样本数据来估计整个学校的总体数据，若从该校(人数很多)任选4人，记表示抽到“goodsight”学生的人数，求的分布列及数学期望．17.如图所示，正方形DDAA11与矩形ABCD所在平面互相垂直，22ADAB，点E为AB的中点.(1)求证：1BD∥平面DEA1；（2）求：DE与面BA11D成角余弦值；（3）在线段AB上是否存在点M，使二面角DMCD1的大小为4？若存在，求出AM的长；若不存在，请说明理由.18．已知数列{an}的前n项和)(2)21(1NnaSnnn，数列{bn}满足.（1）求证数列{bn}是等差数列，并求数列{an}的通项公式；（2）设数列nann1的前n项和为Tn，证明...