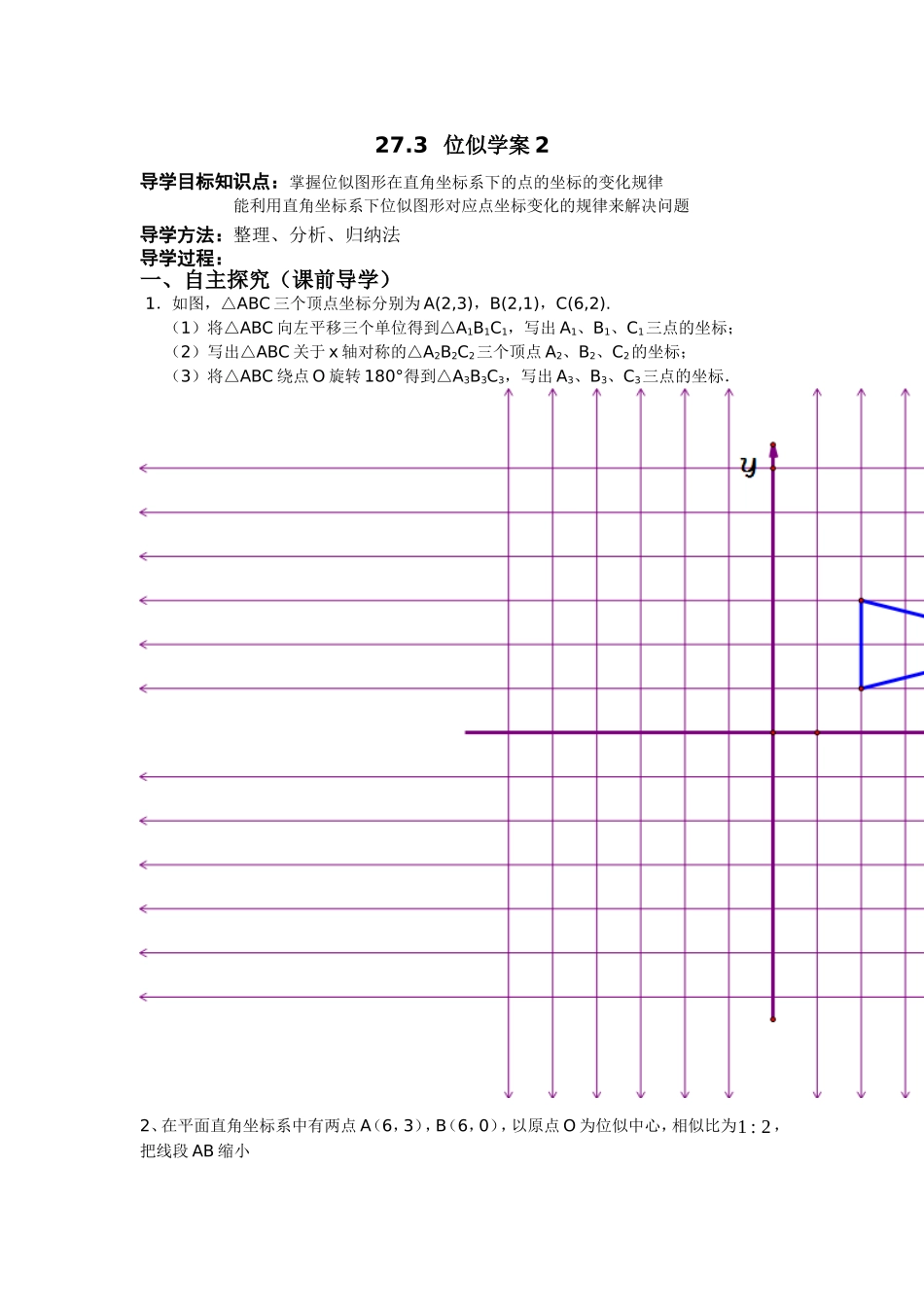
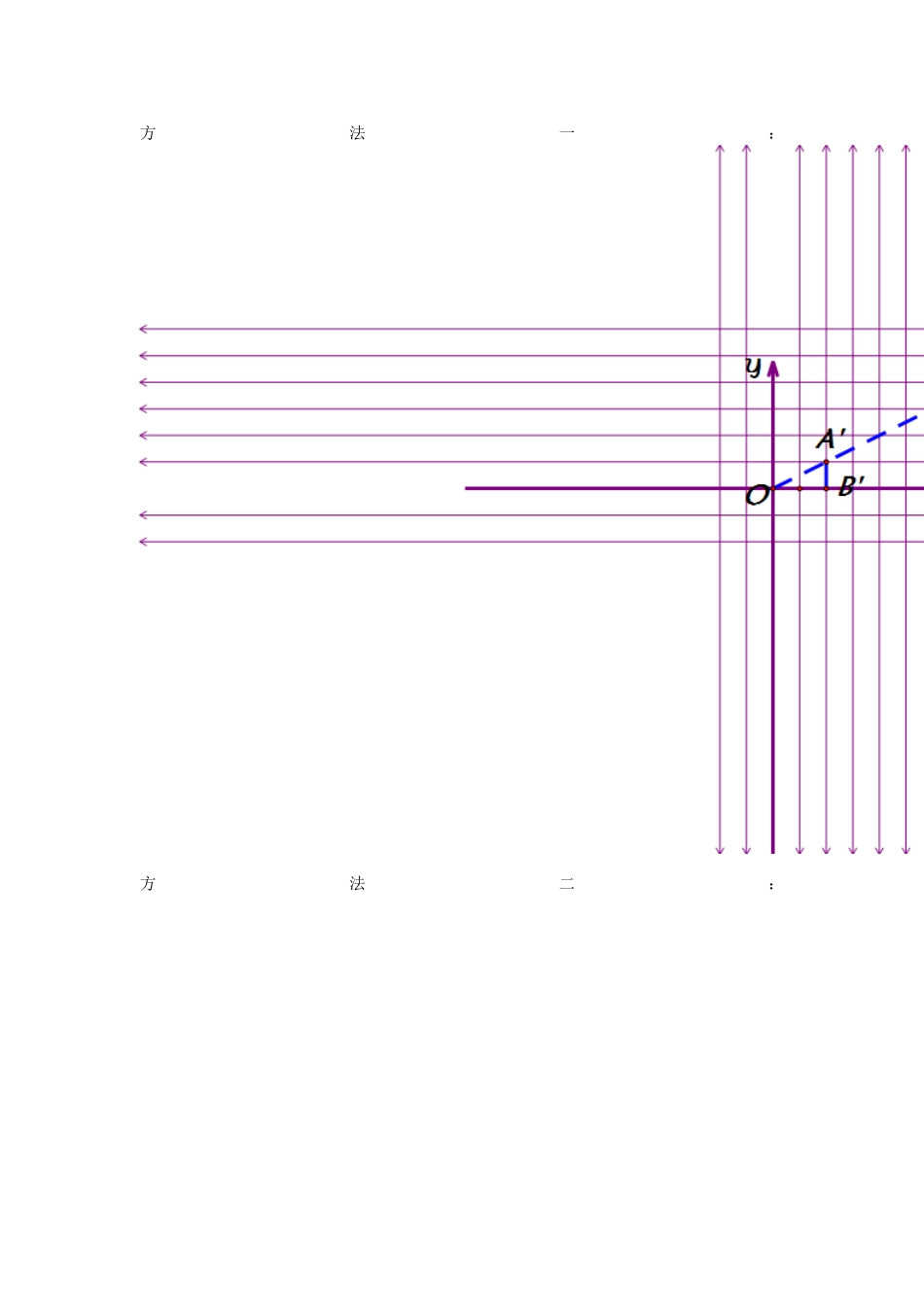
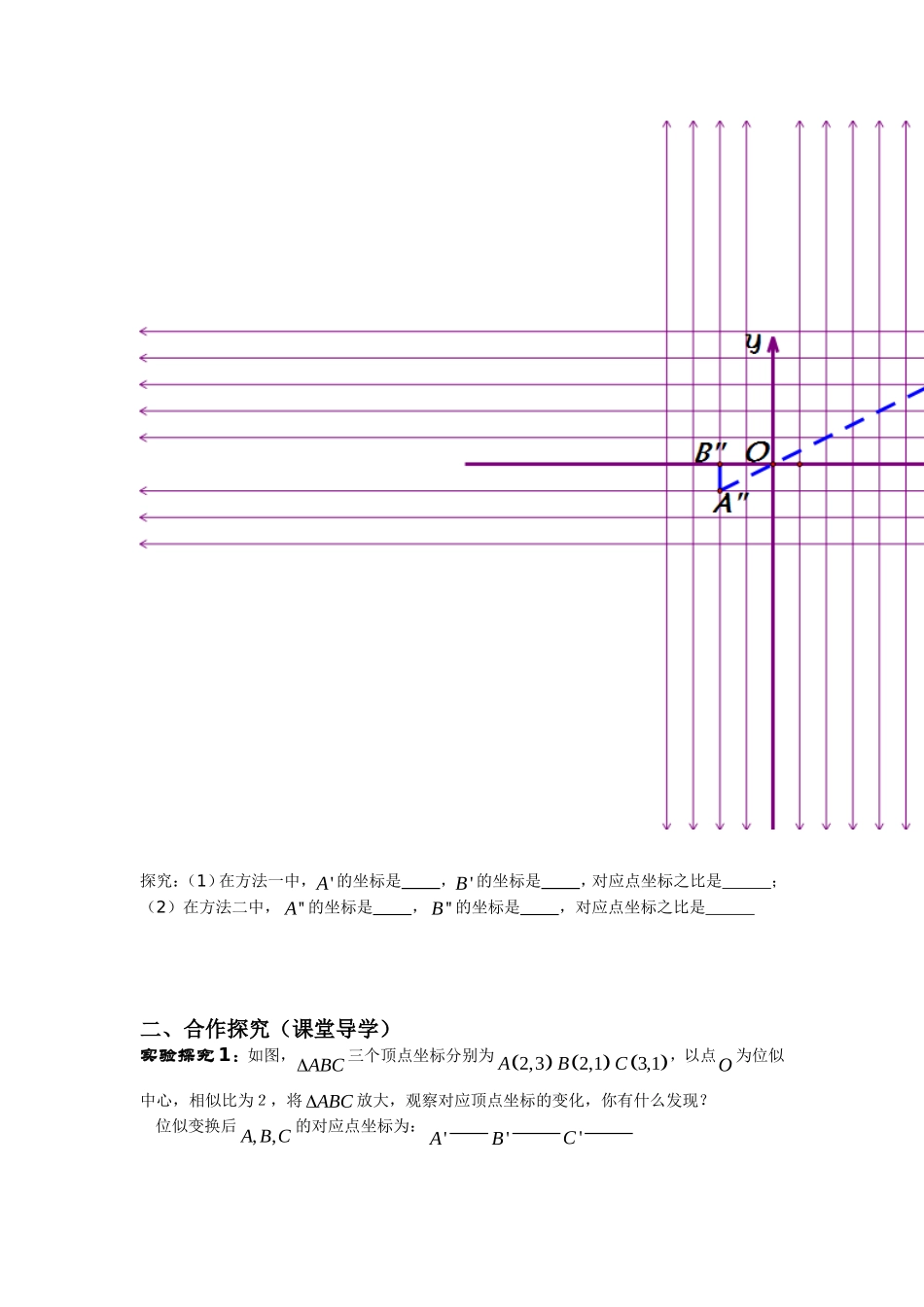
27.3位似学案2导学目标知识点:掌握位似图形在直角坐标系下的点的坐标的变化规律能利用直角坐标系下位似图形对应点坐标变化的规律来解决问题导学方法:整理、分析、归纳法导学过程:一、自主探究(课前导学)1.如图,△ABC三个顶点坐标分别为A(2,3),B(2,1),C(6,2).(1)将△ABC向左平移三个单位得到△A1B1C1,写出A1、B1、C1三点的坐标;(2)写出△ABC关于x轴对称的△A2B2C2三个顶点A2、B2、C2的坐标;(3)将△ABC绕点O旋转180°得到△A3B3C3,写出A3、B3、C3三点的坐标.2、在平面直角坐标系中有两点A(6,3),B(6,0),以原点O为位似中心,相似比为1:2,把线段AB缩小方法一:方法二:探究:(1)在方法一中,'A的坐标是,'B的坐标是,对应点坐标之比是;(2)在方法二中,''A的坐标是,''B的坐标是,对应点坐标之比是二、合作探究(课堂导学)实验探究1:如图,ABC三个顶点坐标分别为2,3A2,1B3,1C,以点O为位似中心,相似比为2,将ABC放大,观察对应顶点坐标的变化,你有什么发现?位似变换后,,ABC的对应点坐标为:'A'B'C归纳:在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于;实验探究2:如图,在平面直角坐标系中,四边形ABCD的坐标分别为A(-6,6),B(-8,2),C(-4,0)D(-2,4)画出一个以原点O为位似中心,相似比为1:2的位似图形。!y!xDBACO三、讨论交流(展示点评)四、课堂检测(当堂训练)如图,在12×12的正方形网格中,△TAB的顶点坐标分别为T(1,1)、A(2,3)、B(4,2).(1)以点T(1,1)为位似中心,按比例尺TA′∶TA=3∶1在位似中心的同侧将△TAB放大为△TA′B′,放大后点A、B的对应点!y!xBTAO分别为A′、B′.画出△TA′B′,并写出点A′、B′的坐标;(2)在(1)中,若C(a,b)为线段AB上任一点,写出变化后点C的对应点C′的坐标.拓展延伸(课外练习):1、如图,与是位似图形,且顶点都在格点上,则位似中心的坐标是_______2、如图,四边形ABCD和四边形A′B′C′D′位似,位似比,四边形A′B′C′D′和四边形A″B″C″D″位似,位似比.四边形A″B″C″D″和四边形ABCD是位似图形吗?位似比是多少?3、如图表示△AOB和把它缩小后得到的△COD,求△COD和△AOB的相似比.!y!xACBDO!y!xC'B'BCAOA'4、如图,△ABC三个顶点坐标分别为A(2,-2),B(4,-5),C(5,-1),以原点O为位似中心,将这个三角形放大为原来的2倍.5、如图,△ABC是格点三角形.在建立平面直角坐标系后,点B的坐标为(-1,-1).(1)把△ABC向左平移5格后得到△A1B1C1,则点B1的坐标为____________(2)把△ABC绕点C按顺时针方向旋转90o后得到△A2B2C,则点B2的坐标为___________(3)把△ABC以点A为位似中心放大,使放大前后对应边长的比为1:2,则B3的坐标是_______6.如图,每个小正方形边长均为1,点O和△ABC的顶点均在小正方形的顶点.(1)以O为位似中心,在网格图中作△A′B′C′和△ABC位似,且位似比为1︰2;(2)连接(1)中的AA′,求四边形AA′C′C的周长.(结果保留根号)!y!xCABOB!y!xACO!yABO