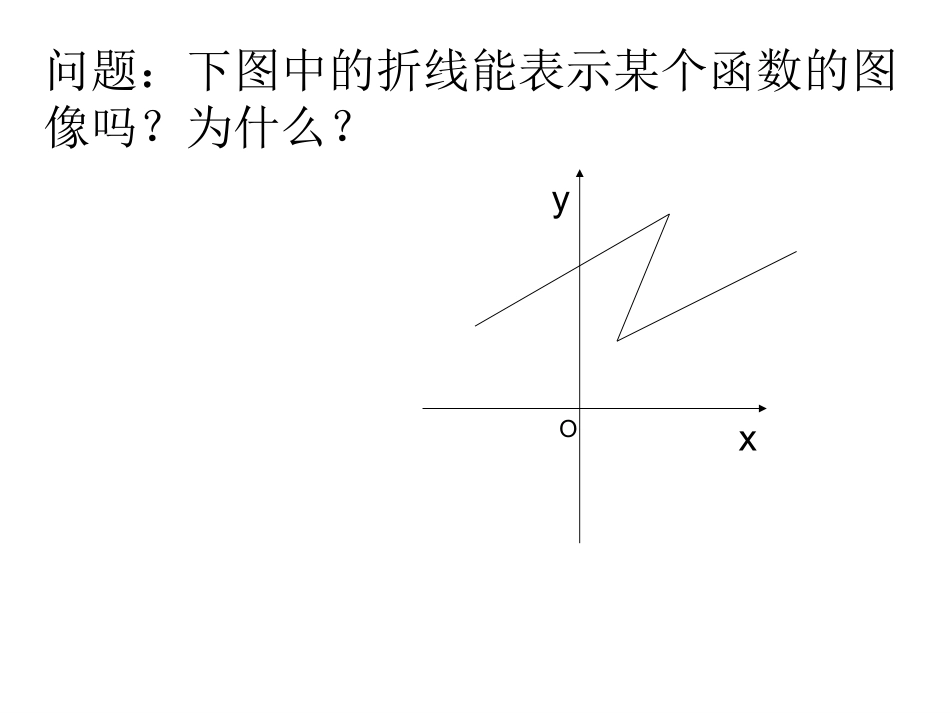
1.2.2函数表示法(2)问题:下图中的折线能表示某个函数的图像吗?为什么?xyO一、函数的图象例1(1)画函数的图象.()2,,||4fxxxRx且若x∈{0,1,2}时函数的图像呢?]0,(x1)0(x1,,,(2)f(x)=(3)、作函数的图象||xyx(4)y=|x|变1:y=|x-2|变2:y=|x|-2概括:y=|f(x)|与y=f(|x|)图象的区别另见作业本T2221001xxRxxxR,,,(5)y=•(6)y=|x-2|+|x+1|•(作图并说出值域)练习P23T2P25B组T1、2例1设周长为20cm的矩形的一边长为xcm,面积为Scm2,那么x与S的对应关系是否为函数?若是,试用适当的方法表示出来.(10),(0,10)Sxxx二、确定函数的解析式练习:(1)已知f(x)是一次函数,且f[f(x)]=9x+8,求f(x);(2)已知f(x)为二次函数,且f(x+1)+f(x–1)=,求f(x).224xx(3)设f(2x–3)=4x+5,求f(x).).(,2)1()4(xfxxxf求已知小结:求函数解析式的常用方法•1、待定系数法•2、配凑法•3、换元法•4、解方程组法•练习:P23T1P24T8、9••P25B组T3、4问题提出1.设集合A={x|x是正方形},B={y|y>0},对应关系f:正方形→面积,那么从集合A到集合B的对应是否是函数?为什么?2.函数是“两个数集A、B间的一种确定的对应关系”,如果集合A、B不都是数集,这种对应关系又怎样解释呢?知识探究(一)考察下列两个对应:AB图1图2AB思考1:上述两个对应有何共同特点?集合A中的任何一个元素,在集合B中都有唯一确定的元素和它对应.思考2:我们把具有上述特点的对应叫做映射,那么如何定义映射?设A、B是两个非空的集合,如果按某一个确定的对应关系f,使对于集合A中的任意一个元素x,在集合B中都有唯一确定的元素y与之对应,那么就称对应f:A→B为从集合A到集合B的一个映射.其中集合A中的元素x称为原象,在集合B中与x对应的元素y称为象.思考3:下图中的对应是不是映射?为什么?AB图1AB图2思考4:在我们的生活中处处有映射,你能举一个实例吗?思考5:函数一定是映射吗?映射一定是函数吗?思考6:图1是从集合A到集合B的一个映射吗?图2是从集合B到集合A的一个映射吗?AB图1AB图2思考7:映射有哪几种对应形式?一对一,多对一总结:•对于映射f:A→B•(1)集合A、B均为非空集合,A中元素不可剩余,B中的元素允许有剩余;•(2)一对一、多对一可以,但一对多不可以;•(3)映射具有方向性,f:A→B和•f:B→A是不同的;•(4)映射也有三要素。理论迁移例1试判断下面给出的对应是否为从集合A到集合B的映射?(1)集合A={P|P是数轴上的点},集合B=R,对应关系f:数轴上的点与它所代表的实数对应;(2)集合A={P|P是平面直角坐标系中的点},集合B={(x,y)|x∈R,y∈R},对应关系f:平面直角坐标系中的点与它的坐标对应;(3)集合A={x|x是三角形},集合B={x|x是圆},对应关系f:每一个三角形都对应它的内切圆;(4)集合A={x|x是师大附中的班级},集合B={x|x是师大附中的学生},对应关系f:每一个班级都对应班里的学生;(5)集合A={1,2,3,4},B={3,4,5,6,7,8,9},对应关系f:x→2x+1课堂练习:P23T4例2已知集合A={a,b},集合B={c,d,e}.(1)试建立一个从集合A到集合B的映射?(2)一共可建立多少个从集合A到集合B的映射?从集合B到集合A的映射呢?例3下列对应关系f是否为从集合A到集合B的函数?22(1),{|0},:||;(2),,:;(3),,:;(4),,:3.ARByyfxxARBRfxxAZBRfxxAZBZfxx22(1),{|0},:||;(2),,:;(3),,:;(4),,:3.ARByyfxxARBRfxxAZBRfxxAZBZfxx22(1),{|0},:||;(2),,:;(3),,:;(4),,:3.ARByyfxxARBRfxxAZBRfxxAZBZfxx本节主要学习内容:1.函数的图象;2.根据已知条件求函数的解析式.3.映射课外作业:作业本的解析式。和求:已知思考)]([)]([{)(,1)(10,10,22xfgxgfxgxxfxxxx思考题2的最小值是则中的较大者,表示,函数对于任意)(34,2123,3)(2xfxxxxxfRx同学们再见下课了例2、21世纪游乐园要建造一个直径为20m的圆形喷水池.如图所示.计划在喷水池的周边靠近水面的位置建一圈喷水头,使喷出的水柱在离池中心4m处达...