两点间的距离教案VIP免费

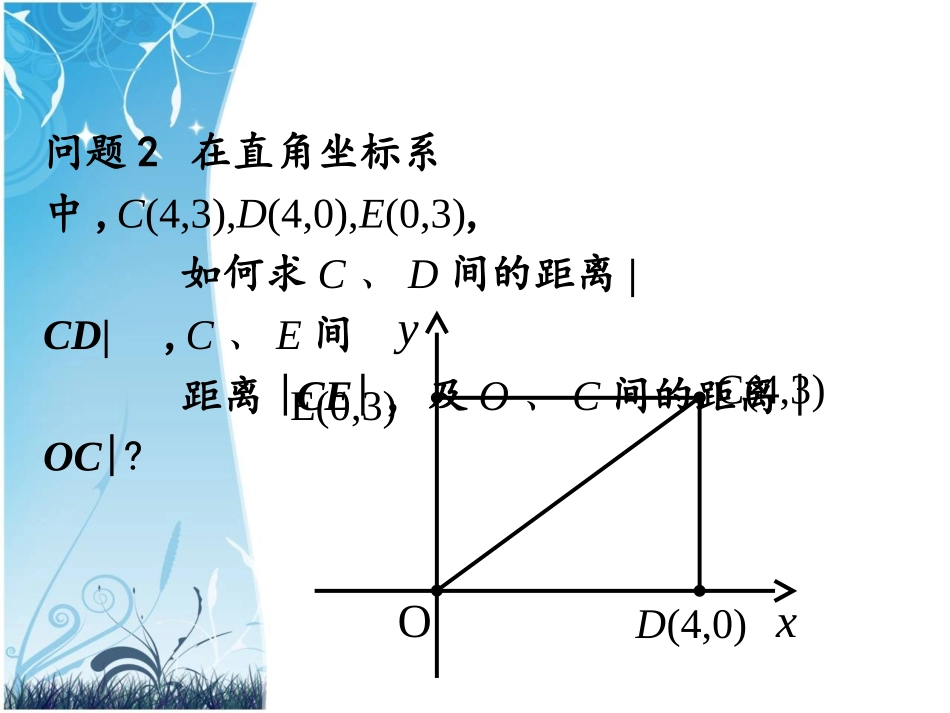
普通高中课程标准实验教科书(人教版)3.3.2两点间的距离问题1：如图，设数轴x上的两点A、B，怎样求A、B之间的距离|AB|？x0ABab问题2在直角坐标系中,C(4,3),D(4,0),E(0,3),如何求C、D间的距离|CD|,C、E间距离|CE|，及O、C间的距离|OC|?yxOC(4,3)D(4,0)E(0,3)问题3已知平面上两点、，如何求间的距离？21PP、111,yxP222,yxPxyO2x1y1x2y111,yxP222,yxPQ12,yxMN解：从P1，P2分别向y轴和x轴作垂线，垂足分别为N(0,y1），M(x2，0)，直线P1N与P2M交于Q点，Q(X2，Y1).在Rt△P1QP2中,|P1P2|2=|P1Q|2+|QP2|2.|P1Q|=|x2-x1|,|QP2|=|y2-y1|.所以，|22122121()()PPxxyy讲授新知两点间的距离公式：22122121()()PPxxyy222111,,yxPyxP、特别地,原点O(0,0)与任一点的距离：yxP,22yxOP1、求下列两点间的距离：(1)、A(6，0),B(-2，0)(2)、A(0，-4),B(0，-1)(3)、A(6，0),B(0，-2)(4)、A(2，1),B(5，-1)巩固练习深化知识例已知点,在x轴上求一点P，使，并求的值．PAPB)7,2()2,1(BA、PA巩固练习深化知识解：设所求点P（x，0），于是有由得解得x=1.所以，所求点P（1，0），且11x4-x7-02-x222）（）（PB，）（）（5x2x2-01x222PAPBPA11x4-x5x2x22222-01122）（）（PA归纳小结反思提高通过本节课的学习，你学到了哪些知识？请谈一谈体会和收获。布置作业分层落实(1)复习本节课的知识，预习下节课的学习内容(2)必做：110页A组6、8题(3)选做：110页B组6题(4)思考：已知一个平行四边形三个顶点的坐标分别为（1,2）、（3，1）、（4,6），怎样求它的第四个顶点的坐标？