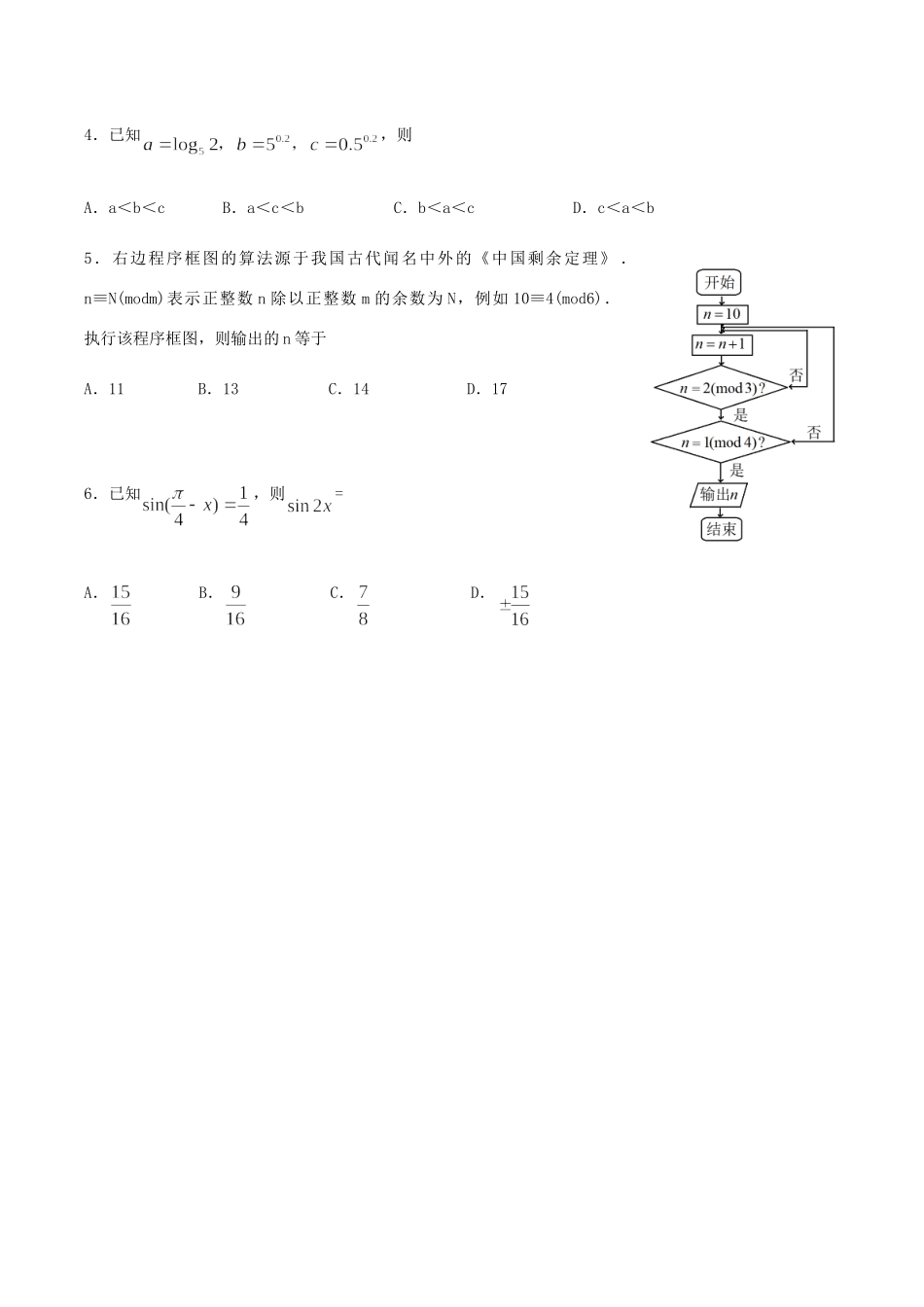
山西省太原市2020届高三数学模拟试题(二)文注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷1至4页,第Ⅱ卷5至8页。2.回答第Ⅰ卷前,考生务必将自己的姓名、准考证号填写在答题卡上。3.回答第Ⅰ卷时,选出每小题答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号,写在本试卷上无效。4.回答第Ⅱ卷时,将答案写在答题卡相应位置上,写在本试卷上无效。5.考试结束后,将本试卷和答题卡一并交回。第Ⅰ卷(选择题共60分)一、选择题:本题共12小题,每小题5分,共60分,在每小题给出的四个选项中.只有一项是符合题目要求的.1.已知集合,,则=A.B.C.D.2.设复数z满足(1-i)·z=i,则=A.B.C.2D.3.等比数列的前n项和为,若=2,=-6,则=A.-22B.-14C.10D.184.已知,则A.a<b<cB.a<c<bC.b<a<cD.c<a<b5.右边程序框图的算法源于我国古代闻名中外的《中国剩余定理》.n≡N(modm)表示正整数n除以正整数m的余数为N,例如10≡4(mod6).执行该程序框图,则输出的n等于A.11B.13C.14D.176.已知,则=A.B.C.D.7.函数的图象大致为8.圆周率π是数学中一个非常重要的数,历史上许多中外数学家利用各种办法对π进行了估算.现利用下列实验我们也可对圆周率进行估算.假设某校共有学生N人.让每人随机写出一对小于1的正实数a,b,再统计出a,b,1能构造锐角三角形的人数M,利用所学的有关知识,则可估计出π的值是A.B.C.D.9.已知,是两个非零向量,其夹角为,若,且,则=A.B.C.D.10.过抛物线的焦点的直线与抛物线交于A,B两点,设点M(3,0).若△MAB的面积为.则|AB|=A.2B.4C.D.811.对于函数.有下列说法:①f(x)的值城为[-1,1];②当且仅当时,函数f(x)取得最大值;③函数f(x)的最小正周期是π;④当且仅当时f(x)>0.其中正确结论的个数是A.①②B.②④C.③④D.①③12.三棱锥P—ABC中.AB⊥BC,△PAC为等边三角形,二面角P—AC—B的余弦值为,当三棱锥的体积最大时,其外接球的表面积为8π.则三棱锥体积的最大值为A.1B.2C.D.第Ⅱ卷(非选择题共90分)本卷包括必考题和选考题两部分,第13题~第21题为必考题,每个试题考生都必须作答.第22题、第23题为选考题,考生根据要求作答.二、填空题:本大题共4小题,每小题5分,共20分.13.若曲线在点处的切线方程为,则=.14.已知双曲线的左、右焦点分别为,点P是双曲线上一点,若为等腰三角形,,则双曲线的离心率为.15.已知△ABC中,a、b、c分别是内角A、B、C的对边,a+c=6,,则△ABC面积的最大值是.16.中国古代教育要求学生掌握“六艺”,即“礼、乐、射、御、书、数”.某校为弘扬中国传统文化,举行有关“六艺”的知识竞赛.甲、乙、丙三位同学进行了决赛.决赛规则:决赛共分6场,每场比赛的第一名、第二名、第三名的得分分别为a,b,c(a>b>c,a,b,c),选手最后得分为各场得分之和,决赛结果是甲最后得分为26分,乙和丙最后得分都为11分,且乙在其中一场比赛中获得第一名,现有下列说法:①每场比赛第一名得分a=4分;②甲可能有一场比赛获得第二名;③乙有四场比赛获得第三名;④丙可能有一场比赛获得第一名.则以上说法中正确的序号是.三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.(一)必考题:共60分.17.(本小题满分12分)已知数列的前n项和为Sn,且满足(Ⅰ)求证:数列是等比数列;(Ⅱ)若.求数列的前n项和Tn.18.(本小题满分12分)按照水果市场的需要等因素,水果种植户把这种成熟后的水果按其直径d的大小分为了不同的等级.某商家计划从该种植户那里购进一批这种水果销售,为了了解这种水果的质量等级情况,随机抽取了100个这种水果,统计得到如下直径分布表:(单位:mm)用分层抽样的方法从其中的一级品和特级品中共抽取6个,其中一级品2个.(Ⅰ)估计这批水果中特级品的比例;(Ⅱ)已知样本中这种水果不按等级混装的话20个约1斤,该种植户有20000斤这种水果...