3.2.2同角三角函数之间的关系VIP免费

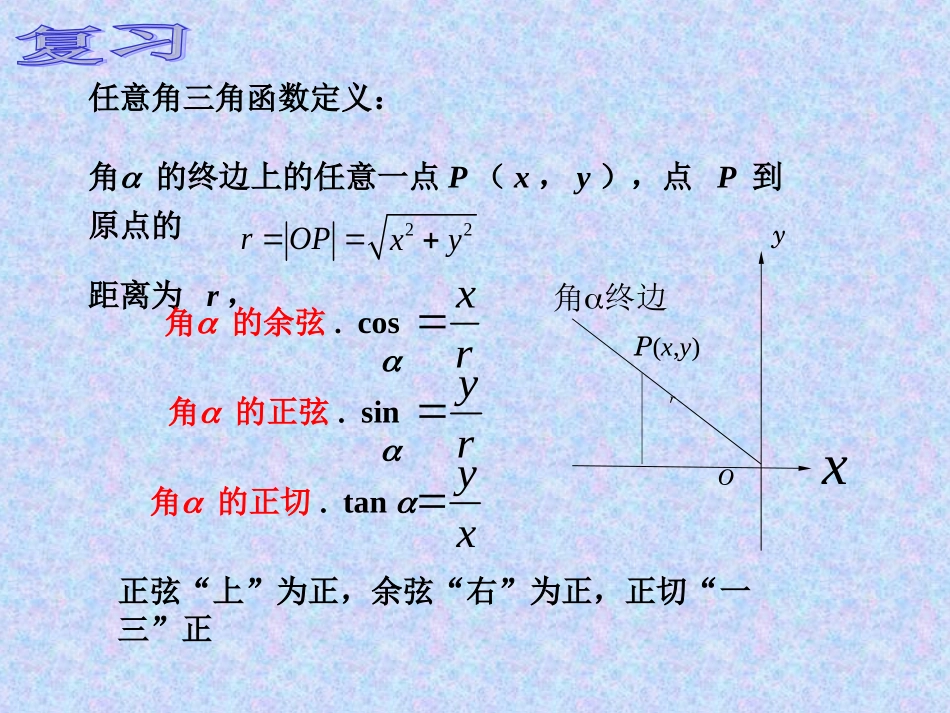
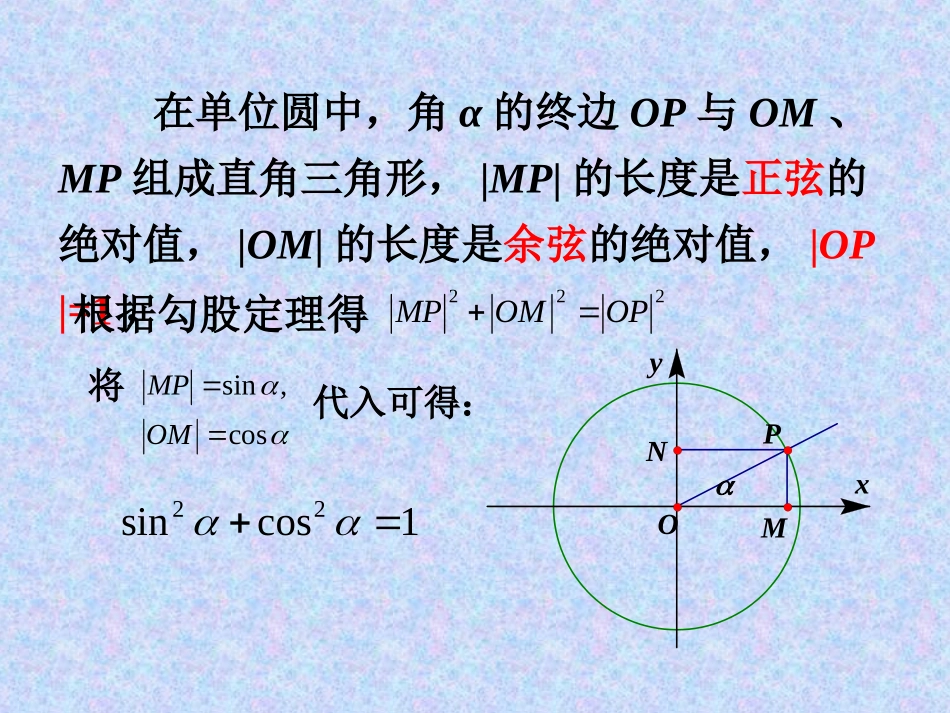
同角三角函数关系式角的终边上的任意一点P（x，y），点P到原点的距离为r，任意角三角函数定义：rxrOP22xy角的余弦.cos角的正弦.sinry角的正切.tanxy角终边xyP(x,y)Or正弦“上”为正，余弦“右”为正，正切“一三”正在单位圆中，角α的终边OP与OM、MP组成直角三角形，|MP|的长度是正弦的绝对值，|OM|的长度是余弦的绝对值，|OP|=1，根据勾股定理得NMPyxO222OPOMMPcos,sinOMMP将代入可得：1cossin22同角三角函数的基本关系式:sintan,cos22sincos1,注意事项：2.公式中的角一定是同角，否则公式可能不成立.如sin230º+cos260º≠1.3.同角不要拘泥于形式α，，6α等等都可.2如sin24α+cos24α=1.1.只有当α的取值使三角函数有意义时，上面恒等式才成立.(1)当我们知道一个角的某一个三角函数值时，可以利用这两个三角函数关系式和三角函数定义，求出这个角的其余三角函数值。同角三角函数关系式的应用：(2)此外，还可用它们化简三角函数式和证明三角恒等式。分析：由平方关系可求cosα的值，由已知条件和cosα的值可以求tanα的值，例1已知，且α在第三象限，求53sincostan和解：∵sin2α+cos2α=1，α是第二象限角.54531sin1cos2243cossintan为第三或第四象限角解：,0sin43tan54sin1cos43tan54sin1cos1cossin2222在第四象限时，当在第三象限时，当得，由变式：.tancos,53sin和求已知53sin,54,2516cos1cossin,cos43sin43tan,cossintan222cos是第二象限的角所以又因为得代入得解：由正弦值和余弦值。的求角是第二象限的角，，且已知43-tan例2、例3.已知sinα－cosα=,180º<α<270º.求tanα的值。55解：以题意和基本三角恒等式，得到方程组225sincos5sincos1消去sinα，得5cos2α－cosα－2=0，5由方程解得cosα=255或cosα=55因为180º<α<270º，所以cosα<0，即cosα=55代入原方程组得sinα=255于是tanα==2.sincos变式：已知求的值,51cossincossin.例4解：tan3已知，4sin2cos1;5cos3sin（）22(3)2sinsincos3cos.1（）原式4tan253tan5.7求下列各式的值：21(2);2cossincos432533(2)=原式222sincos2cossincos2tan12tan110.7(3)原式222tantan3tan1222333319.5222sinsincos3cos122222sinsincos3cossincos解：2222=2sinsincos3cos2(sincos)原式224sinsincoscos122=4sinsincoscos224tantan1tan12243313119.5练习：tan3已知，22(1)2sinsincos3cos2;求下列各式的值33sin2cos(2).cos3sin22224sinsincoscossincos857原式1sincos3已知，求下列各式的值：331(1)tan;(2)sincos.tan解:sincos1(1)tantancossin22sincoscossin1cossin1sincos3，由得21(sincos)9，4sincos,9112sincos9，91tan.tan433(2)sincos22(sincos)(sinsincoscos)(sincos)(1sincos)14(1)3913.27例5：例6.化简下列各式：211sin440（）；212sin20cos20.（）解：211sin440（）21sin(36080)21sin802cos80cos80.212sin20cos20（）2(sin20-cos20)oo|sin20cos20|22sin20cos202sin20cos20|cos80|cos20sin20.：证法1xxxxcossin1sin1cos求证：1sin0cosxx知，由01sinx即)sin1(sin1)sin1(cosxxxx）（左边xxx2sin1)sin1(cosxxx2cos)sin1(cosxxcossin1右边.原等式成立例7小结：1.已知一角的某一三角函数值，求其它的三角函数值2.三角函数式的化简求值3.三角恒等式的证明