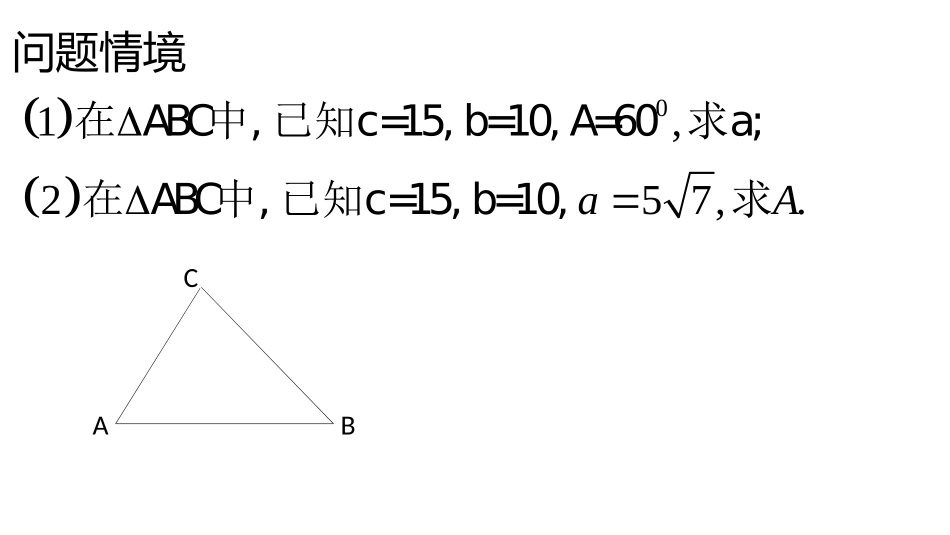
1.2.1余弦定理江苏省奔牛高级中学蒋亦苏教版必修5(高一数学)引入:用正弦定理可以解两类三角形(1)已知两角一边(2)已知两边及其一边对角AAS,ASASSA唯一不确定问题1:根据三角形全等的知识,还有哪些类型的三角形也是确定的?SAS,SSS追问:能用正弦定理解吗?(以SAS为例)sinsinsincABabC问题情境01,257,.aA在ABC中,已知c=15,b=10,A=60求a;在ABC中,已知c=15,b=10,求ABC一般的,ABC在中,已知b,c,A,如何表示a?ABCD余弦定理符号:文字:三角形任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍。追问1:观察余弦定理三个公式,他们有何结构特征?追问2:两边及其夹角余弦的乘积,与哪个知识有关?问题2:试用向量数量积证明ABC请用余弦定理求解:01,257,.caA在ABC中,已知c=15,b=10,A=60求;在ABC中,已知c=15,b=10,求小结:余弦定理可以解决哪些类型三角形?(1)已知三边,求三个角;(2)已知两边及夹角,求第三边和其他两个角;追问:常见可解三角形类型及其方法?(3)已知两边及其一边对角,222222;.abcabc例2.用余弦定理证明:当C锐角时,当C钝角时,小结:设是最长的边,则a课堂小结一个定理,两种证法;一个推论,两种应用余弦定理可以解决的有关三角形的问题:1、已知两边及其夹角,求第三边和其他两个角。2、已知三边求三个角;3、判断三角形的形状