1.3一元二次方程的根与系数的关系 (3)VIP免费

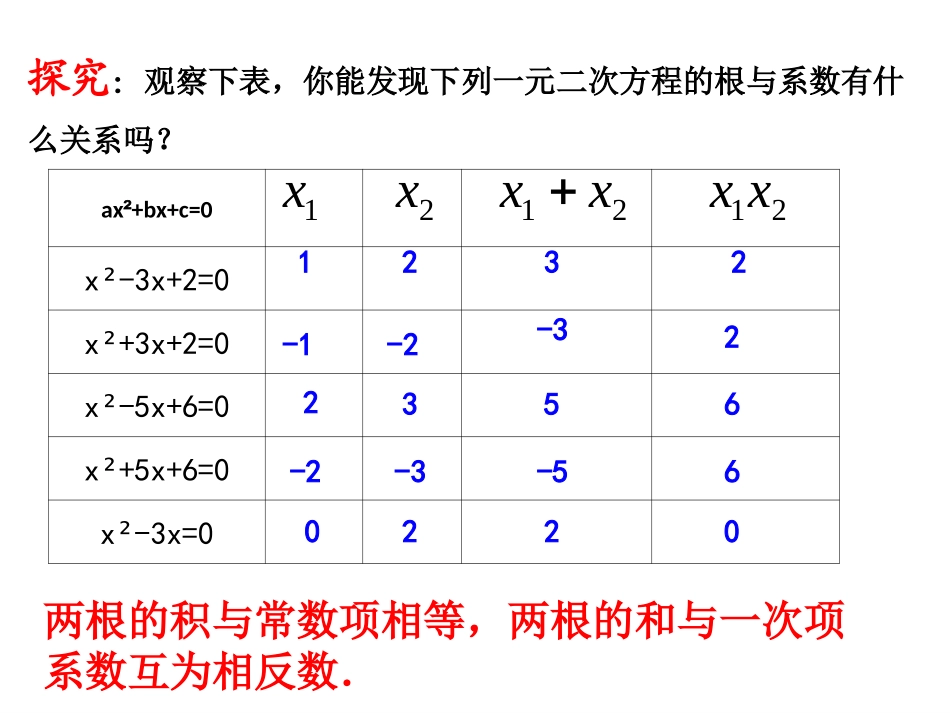
1.3一元二次方程的根与系数的关系ax²+bx+c=0x-3x+2=0²x+3x+2=0²x-5x+6=0²x+5x+6=0²x-3x=0²1x2x21xx21xx12322-2-3-16352-2-3-560220探究：观察下表，你能发现下列一元二次方程的根与系数有什么关系吗？两根的积与常数项相等，两根的和与一次项系数互为相反数．【解释规律】你能解释刚才的发现吗？你能解释刚才的发现吗？1.3一元二次方程的根与系数的关系1.3一元二次方程的根与系数的关系22124422bbacbbacxxaa，22124422bbacbbacxxaa．则则一元二次方程ax2＋bx＋c＝0（a≠0），如果b2－4ac≥0，它的两个根分别是x1、x2．1.3一元二次方程的根与系数的关系1.3一元二次方程的根与系数的关系22124422bbacbbacxxaa＋＋＝＋22442bbacbbaca＝22ba＝ba＝．1.3一元二次方程的根与系数的关系1.3一元二次方程的根与系数的关系22124422bbacbbacxxaa＝22244bbaca＝244aca＝ca＝．【总结发现】1.3一元二次方程的根与系数的关系1.3一元二次方程的根与系数的关系如果方程ax2+bx+c=0(a≠0)的两个根是x1,x2,那么x1+x2=,x1x2=ab-ac注：能用公式的前提条件为b2-4ac≥0在使用根与系数的关系时，应注意：⑴不是一般式的要先化成一般式；⑵在使用X1+X2=－时，注意“－”不要漏写。ab如果方程x2+px+q=0的两根是X1，X2，那么X1+X2=,X1X2=.－Pq一元二次方程根与系数的关系是法国数学家“韦达”发现的,所以我们又称之为韦达定理.说出下列各方程的两根之和与两根之积：(1)x2-2x-1=0(3)2x2-6x=0(4)3x2=4(2)2x2-3x+=021x1+x2=2x1x2=-1x1+x2=x1+x2=3x1+x2=0x1x2=x1x2=0x1x2=-2341341.3一元二次方程的根与系数的关系1.3一元二次方程的根与系数的关系【例题精讲】例1、已知方程x2-(k+1)x+3k=0的一个根是2,求它的另一个根及k的值.解法一：设方程的另一个根为x2.由韦达定理，得2＋x2=k+12x2=3k解这方程组，得x2=－3k=－2答：方程的另一个根是－3,k的值是－2.例1、已知方程x2-(k+1)x+3k=0的一个根是2,求它的另一个根及k的值。解法二：设方程的另一个根为x2.把x=2代入方程，得4-2(k+1)+3k=0解这方程，得k=-2由韦达定理，得2x2＝3k即2x2＝－6∴x2＝－3答：方程的另一个根是－3,k的值是－2.1、已知方程3x2－19x+m=0的一个根是1，求它的另一个根及m的值。2、设x1,x2是方程2x2＋4x－3=0的两个根，求(x1+1)(x2+1)的值.解：设方程的另一个根为x2,319则x2+1=,∴x2=,316又x2●1=,3m∴m=3x2=16解：由韦达定理,得x1+x2=-2,x1·x2=23∴(x1+1)(x2+1)=x1x2+(x1+x2)+1=-2+()+1=2325【尝试与交流】1.3一元二次方程的根与系数的关系1.3一元二次方程的根与系数的关系你能写出这个方程中被墨迹污染的一次项系数和常数项吗？你能写出这个方程中被墨迹污染的一次项系数和常数项吗？小明在一本课外读物中读到如下一段文字：一元二次方程x2－x＝0的两根是和．小明在一本课外读物中读到如下一段文字：一元二次方程x2－x＝0的两根是和．2323已知关于x的方程x2+(2m-1)x+m2=0有两个实数根x1、x2.（1）求实数m的取值范围；（2）当x12-x22=0时，求m的值.拓展与延伸拓展与延伸【练习】课本练习P23练习1、2．课本练习P23练习1、2．1.3一元二次方程的根与系数的关系1.3一元二次方程的根与系数的关系【小结】2．应用一元二次方程的根与系数关系时，首先要把方程化成一般形式；3．应用一元二次方程的根与系数关系时，要特别注意，方程有实根的条件，即当且仅当b2－4ac≥0时，才能应用根与系数的关系.1．一元二次方程根与系数的关系是什么?1.3一元二次方程的根与系数的关系1.3一元二次方程的根与系数的关系【课后作业】课本习题1.3．课本习题1.3．1.3一元二次方程的根与系数的关系1.3一元二次方程的根与系数的关系