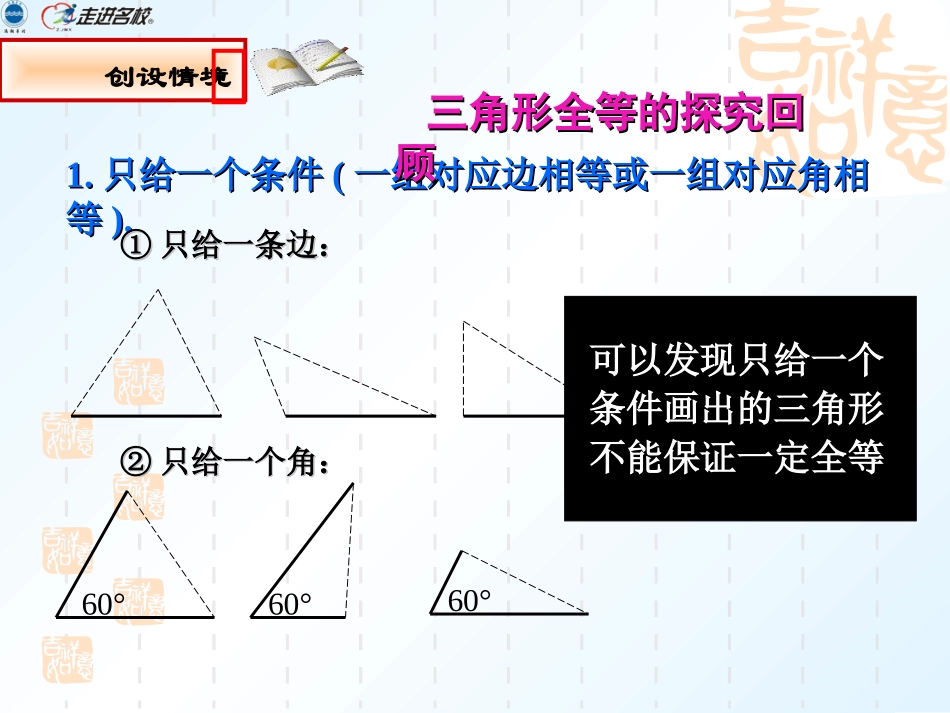
11.2全等三角形的判定④学习目标预习探路1.我们已经学过那些判定两个三角形全等的方法?2.利用角角边和角角角能判定两个三角形全等吗?3、在利用各个判定时要注意什么问题?1、掌握全等三角形的各种判定方法,能根据题目合理选择方法证两个三角形全等。2、掌握利用全等三角形证线段或角相等的方法。1.1.只给一个条件只给一个条件((一组对应边相等或一组对应角相一组对应边相等或一组对应角相等等).).①①只给一条边:只给一条边:②②只给一个角:只给一个角:60°60°60°可以发现只给一个可以发现只给一个条件画出的三角形条件画出的三角形不能保证一定全等不能保证一定全等三角形全等的探究回三角形全等的探究回顾顾创设情境2.2.给出两个条件:给出两个条件:①①一边一内角:一边一内角:②②两内角:两内角:③③两边:两边:30°30°30°30°30°50°50°2cm2cm4cm4cm可以发可以发现给出两个条件时现给出两个条件时画出的三角形也不画出的三角形也不能保证一定全等。能保证一定全等。三边对应相等的两个三角形全等(可以简写为“边边边”或“SSS”)。ABCDEF在△ABC和△DEF中∴△ABCDEF≌△(SSS)AB=DEBC=EFCA=FD用符号语言表达为:用符号语言表达为:三角形全等判定方法三角形全等判定方法11创设情境三角形全等判定方法三角形全等判定方法22用符号语言表达为:用符号语言表达为:在△ABC与△DEF中∴△ABCDEF≌△(SAS)两边和它们的夹角对应相等的两个三角形全等。(可以简写成“边角边”或““SASSAS””))FEDCBAAC=DF∠C=F∠BC=EF∠A=D∠(已知)AB=DE(已知)∠B=E∠(已知)在△ABC和△DEF中∴△ABCDEF△(ASA)有两角和它们夹边对应相等的两个三角有两角和它们夹边对应相等的两个三角形全等形全等((可以简写成“角边角”或“可以简写成“角边角”或“ASAASA””)。)。用符号语言表达为:用符号语言表达为:FEDCBA三角形全等判定方法三角形全等判定方法33思考思考:在△ABC和△DFE中,当∠A=D,C=F∠∠∠和AB=DE时,能否得到△ABCDFE?≌△三角形全等判定方法三角形全等判定方法44有两角和其有两角和其中一个角的对边对应相中一个角的对边对应相等的两个三角形全等等的两个三角形全等((可以简写成“角可以简写成“角边角”或“边角”或“AASAAS””)。)。CBAFEDDCBAABDABCABDABCSSASSA不不能判定全能判定全等等创设情境思考:三个角对应相等的两个三角形全等吗?例例1:1:如图如图,,点点BB在在AEAE上上,CAB=DAB,∠∠,CAB=DAB,∠∠要使要使ΔABCΔABD,≌ΔABCΔABD,≌可补充的一可补充的一个条件是个条件是..EDCBA分析:现在我们已知分析:现在我们已知AA→CAB=DAB∠∠→CAB=DAB∠∠①①用用SAS,SAS,需要补充条需要补充条件件AB=AC,AB=AC,②②用用ASA,ASA,需要补充条需要补充条件件∠∠CBA=DBA,∠CBA=DBA,∠③③用用AAS,AAS,需要补充条需要补充条件件∠∠C=D,∠C=D,∠④④此外此外,,补充条件补充条件∠∠CBE=DBE∠CBE=DBE∠也可以也可以(?)(?)SASSASASAASAAASAASSS→AB=AB(→AB=AB(公共边公共边).).AB=ACAB=AC∠∠CBA=DBA∠CBA=DBA∠∠∠C=D∠C=D∠∠∠CBE=DBE∠CBE=DBE∠理性提升例例2:2:如图如图,AE=AD,,AE=AD,要要使使ΔABDΔACE,≌ΔABDΔACE,≌请请你增加一个条件是你增加一个条件是..EDCBA分析分析::现在我们已知现在我们已知SS→AE=AD→AE=AD①①用用SAS,SAS,需要补充条需要补充条件件AB=AC,AB=AC,②②用用ASA,ASA,需要补充条需要补充条件件∠∠ADB=AEC,∠ADB=AEC,∠③③用用AAS,AAS,需要补充条需要补充条件件∠∠B=C,∠B=C,∠④④此外此外,,补充条件补充条件∠∠BDC=BEC∠BDC=BEC∠也可以也可以(?)(?)SASSASASAASAAASAAS(CD=BE(CD=BE行吗行吗?)?)AA→A=A(∠∠→A=A(∠∠公共公共角角).).理性提升例4:如图,已知△ABC中,BE和CD分别为∠ABC和∠ABC的平分线,且BD=CE,∠1=∠2,求证:BE=CD。ABCED12理性提升判定两条线段相等或二个角相等可以通过从它们所在的两个三角形全等而得到。于是本题可以考虑证BD,CE所在的△BEC与△CDB全等.方法构想例2:如图,已知△ABC中,BE和CD分别为∠ABC和∠ABC的平分线,且BD=CE,∠1=∠2,求证:BE=CD。解: ∠DBC=2∠1,∠ECB=2∠2(...