3.1.1两角和与差的余弦-(2)VIP免费

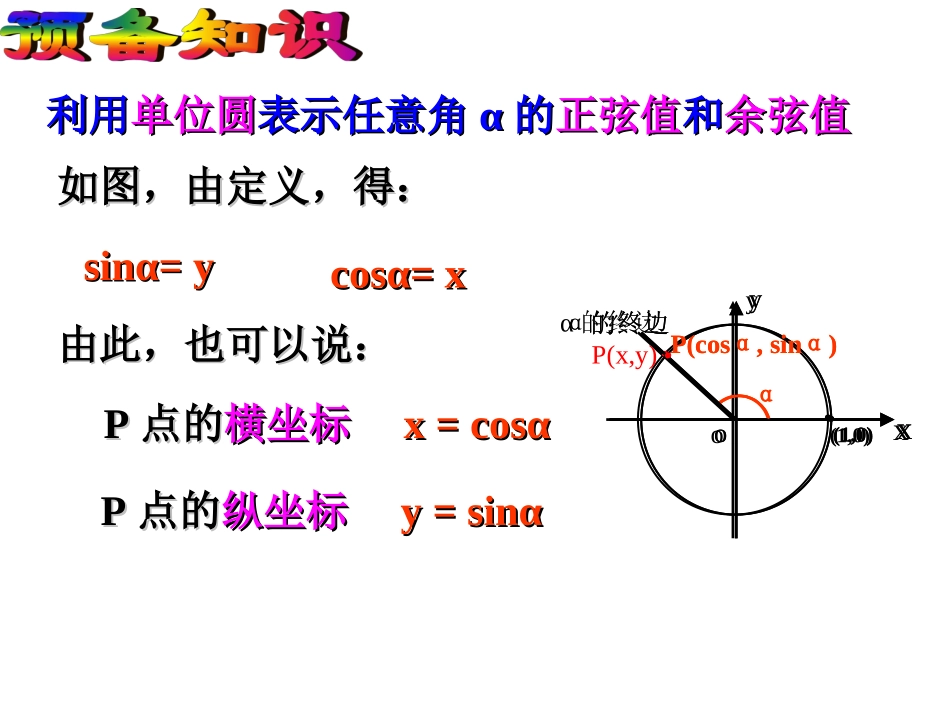
利用利用单位圆单位圆表示任意角表示任意角αα的的正弦值正弦值和和余弦值余弦值yxoP(x,y)(1,0)．α的终边．如图，由定义，得：如图，由定义，得：sinα=ysinα=ycosα=xcosα=x由此，也可以说：由此，也可以说：PP点的点的横坐标横坐标x=cosαx=cosαPP点的点的纵坐标纵坐标y=sinαy=sinαyxoP(cosα,sinα)(1,0)．α的终边．αyxoP(cosα,sinα)(1,0)．α的终边．αOyxBA∴cos(75°-15°)=cos75°cos15°+sin75°sin15°设向量aa＝(cos75°,sin75°),向量bb=(cos15°,sin15°),试分别计算aa·bb=|aa||bb|cosθ及aa·bb=x1x2+y1y2.比较两次计算的结果，你能发现什么？(必修4P83，15)aa·bb=|aa||bb|cos(75°-15°)=cos(75°-15°)aa·bb=x1x2+y1y2=cos75°cos15°+sin75°sin15°问题探究??如何用任意角α与β的正弦、余弦来表示cos(α-β)？思考：你认为会是cos(α-β)=cosαcosβ+sinαsinβ吗?江苏省锡东高级中学谢晓丰两角和与差的余弦-111-1α-βBAyxoβαcossinOA�α,αcossinOB�β,β)cos(OBOAOBOA)cos(OBOAsinsincoscos∵∴cos(α-β)=cosαcosβ+sinαsinβCα-β差角的余弦公式结论归纳α,β对于任意角cos()coscossinsinα-βαβ+αβ注意：1.公式的结构特点；2.对于α,β,只要知道其正弦或余弦，就可以求出cos(α－β)不查表,求cos(–375°)的值.解:cos(–375°)=cos15°=cos(45°–30°)=cos45°cos30°+sin45°sin30°23212222624应用举例分析:cos15cos4530cos15cos6045思考：你会求的值吗?sin75.利用差角余弦公式求的值cos15学以致用！！cos(α-β)=cosαcosβ+sinαsinβ公式的结构特征:左边是复角α-β的余弦,右边是单角α、β的余弦积与正弦积的和.)cos()sin(sin)cos(cos))(cos(sinsincoscos将替换为cos(α+β)=cosαcosβ-sinαsinβ简记：)(C)cos(sinsincoscos两角和与差的余弦公式：结论归纳例4.已知2cos,3α=-α5求的值.cos4α练习:课本P93页练习1,2,3课堂练习223ABCsinAsinB53cos132cos62cos15-sin15__=cosAcosB,ABC().(A)(B)(C)(D)_____1、已知＝－，，，则＋的值是＿＿＿＿；、在中，若则是直角三角形钝角三角形锐角三角、形；不确定思考题：已知都是锐角,，αβcos，4α=55cos13α+βcos求的值ββ=α+βα变角:分析：coscossinαβαsincosαβαcos531312541356516•1.cos(α+β)=cosαcosβ–sinαsinβcos(α–β)=cosαcosβ+sinαsinβ小结•2.利用公式可以求非特殊角的三角函数值,•化简三角函数式和证明三角恒等式。使用•公式时要灵活使用，并要注意公式的逆向•使用.