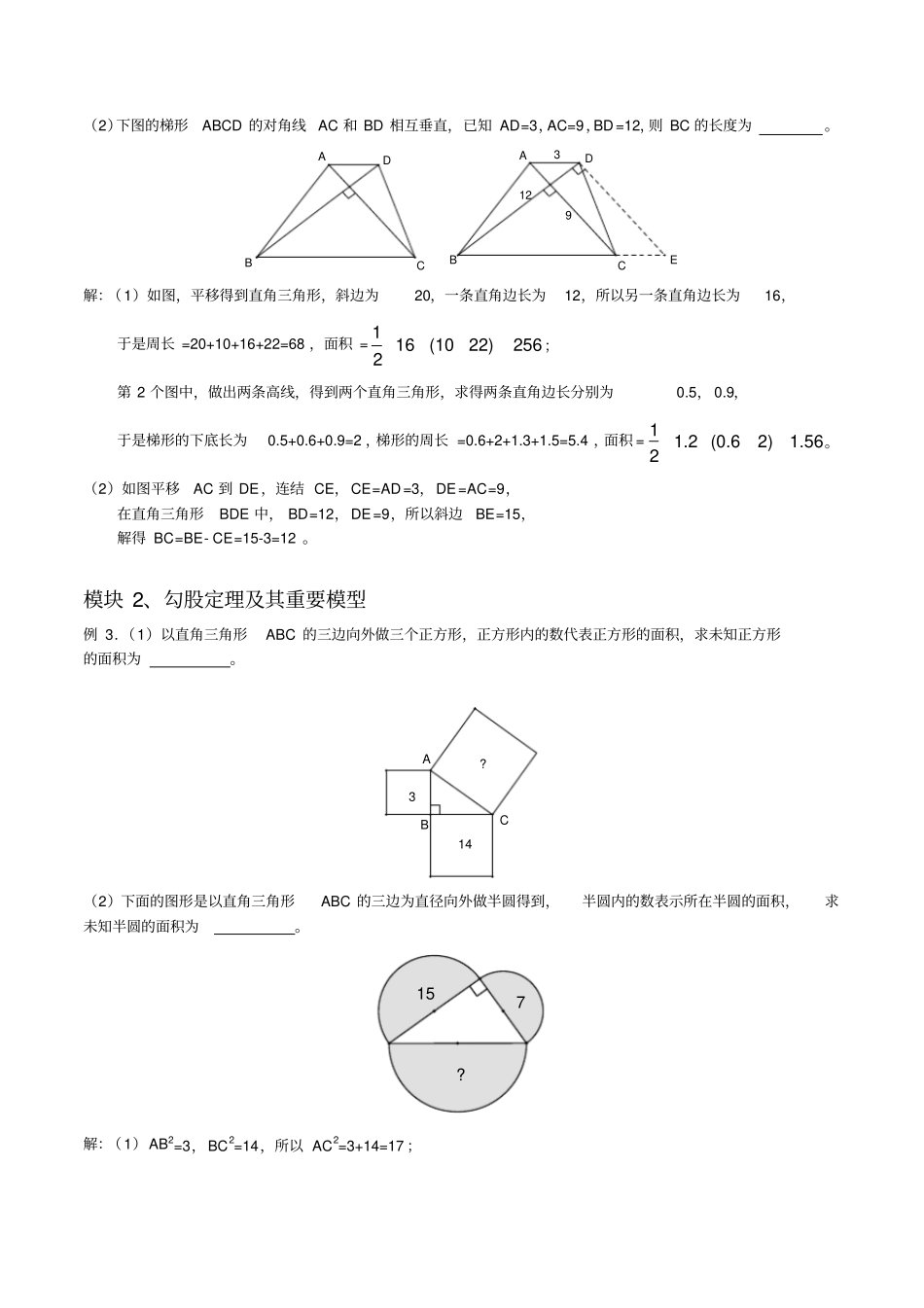
第一讲勾股定理模块1、常见勾股数及辅助线例1.(1)如图,下列未知边的长度分别是、、。(2)如图,下列图形的面积分别是、、。解:(1)应用勾股定理:第1个直角三角形中两条直角边分别是3和4,所以斜边长为5;第2个直角三角形中斜边长为13,一条直角边长为5,所以另一条直角边的长为12;第3个直角三角形中,斜边长为25,一条直角边长为24,所以另一条直角边的长为7。(2)第1个直角三角形的斜边长为10,一条直角边长为8,另一条直角边长为6,所以三角形的面积是186242;第2个直角三角形的斜边长为1.3,一条直角边长为1.2,另一条直角边长为0.5,所以三角形的面积是11.20.50.32;第3的图形中,小直角三角形的两条直角边分别为2和1.5,它的面积是S1=1.5,斜边长为2.5,大直角三角形的斜边是6.5,一条直角边长为2.5,所以另一条直角边长为6,面积S2=12.567.52,于是面积等于S1+S2=9.例2.(1)如左图,梯形的周长为,面积为;如右图,梯形的周长为,面积为;???2524135431081.31.20.61.51.21.320221016122022100.60.50.90.61.51.21.36.51.52(2)下图的梯形ABCD的对角线AC和BD相互垂直,已知AD=3,AC=9,BD=12,则BC的长度为。解:(1)如图,平移得到直角三角形,斜边为20,一条直角边长为12,所以另一条直角边长为16,于是周长=20+10+16+22=68,面积=116(1022)2562;第2个图中,做出两条高线,得到两个直角三角形,求得两条直角边长分别为0.5,0.9,于是梯形的下底长为0.5+0.6+0.9=2,梯形的周长=0.6+2+1.3+1.5=5.4,面积=11.2(0.62)1.562。(2)如图平移AC到DE,连结CE,CE=AD=3,DE=AC=9,在直角三角形BDE中,BD=12,DE=9,所以斜边BE=15,解得BC=BE-CE=15-3=12。模块2、勾股定理及其重要模型例3.(1)以直角三角形ABC的三边向外做三个正方形,正方形内的数代表正方形的面积,求未知正方形的面积为。(2)下面的图形是以直角三角形ABC的三边为直径向外做半圆得到,半圆内的数表示所在半圆的面积,求未知半圆的面积为。解:(1)AB2=3,BC2=14,所以AC2=3+14=17;DCBA1293ECBADCBA?143157?(2)最小的半圆面积等于2r12=7,第二个半圆面积等于2r22=15,所以最大的半圆的面积等于2(r12+r22)=7+15=22.例4.(1)下图是由两个直角三角形构成,求问号处的边长是。(2)下图是由一个两条直角边长都是1的直角三角形向外做直角三角形得到的,形成一共一个美丽的螺旋图案,第8个直角三角形的斜边长是;如果一直螺旋下去,第个直角三角形的斜边长是10.解:(1)由勾股定理,下面的直角三角形的两条直角边长分别为1、2,斜边的平方=1+4=5,这样上面的直角三角形的两条直角边的平方分别是5、4,它们的和等于9,所以问号处的边长等于3.(2)最小的直角三角形的斜边长的平方,等于2,第2个直角三角形的斜边的平方等于3,第3个直角三角形的斜边的平方等于4,⋯⋯,第8个直角三角形的斜边的平方等于9,斜边长等于3,第n个直角三角形的斜边的平方等于102=100,所以这是第99个直角三角形。例5.(1)某直角三角形三条边长都是整数,其中一条直角边长是8,求另外两条边的长度分别为和。(2)某直角三角形的一条直角边长为6,周长是15,求它的面积为。(3)如图,长方形ABCD的长是5,宽是1,现将长方形的右下角折到左上角,三角形ABM的面积是。解:(1)设斜边长为a,另一条直角边的长为b,所以a2-b2=64,得64=(a+b)(a-b),64=26,又a+b、a-b都是整数,且a+b与a-b同奇同偶,221?1111111111NMDCBA5所以可以是322abab,或164abab,解得1715ab或106ab。(2)直角三角形的一条直角边长为6,周长是15,设斜边为a,则另一条直角边是9-a,得2236(9)aa,解得a=6.5,9-a=2.5,所以三角形的面积=162.57.52;(3)设BM=a,MC=5-a,AM=MC=5-a,在直角三角形ABM中,有勾股定理得AM2=AB2+BM2,得22(5)1aa,解得a=2.4,所以三角形ABM的面积=112.41.22。模块3有趣的路径问题例6.(1)如图是一个铁丝围成的长方体铁架,长、宽、高分别为7厘米、2厘米、3厘米,一只蚂蚁在A点,蚂蚁需要爬到B点处,如果只能沿着长方体的棱爬,最短路径是厘米。(2)如图是一个长方体木块,长、宽、高分别为9厘米、7厘米、5厘米,一只蜘...