理论力学--第2章 平面任意力系VIP免费

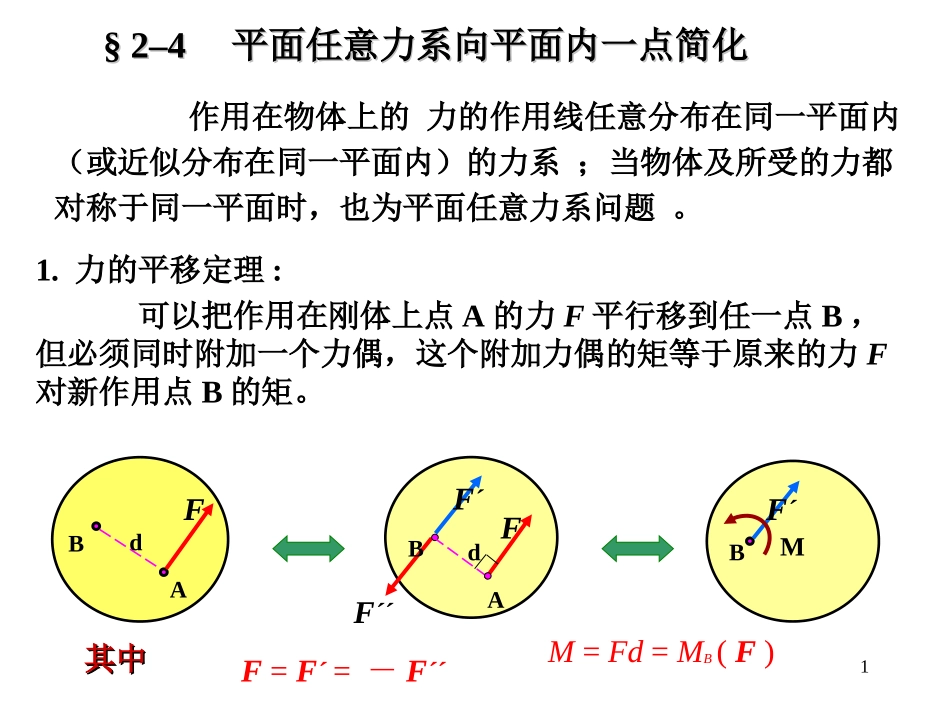
1§2–4§2–4平面任意力系向平面内一点简化平面任意力系向平面内一点简化1.力的平移定理:可以把作用在刚体上点A的力F平行移到任一点B，但必须同时附加一个力偶，这个附加力偶的矩等于原来的力F对新作用点B的矩。其中其中F=F´=－F´´BF´MABFdF´F´´BAFdM=Fd=MB(F)作用在物体上的力的作用线任意分布在同一平面内（或近似分布在同一平面内）的力系；当物体及所受的力都对称于同一平面时，也为平面任意力系问题。22.平面任意力系向作用面内一点简化•主矢和主矩oMF1F2oFnoFn´MnF1´M1F2´M2任意点O为简化中心F1´=F1，F2´=F2，…，Fn´=FnMi=Mo(Fi)(i=1，2，…，n)平面任意力系等效为两个简单力系：平面汇交力系和平面力偶系。FR´3Mo=M1+M2+…+Mn=FR´——主矢Mo——主矩平面任意力系向作用面内任一点O简化，可得一个力和一个力偶。这个力等于该力系的主矢，作用线通过简化中心O。这个力偶的矩等于该力系的主矩。平面汇交力系可合成为作用线通过点O的一个力FR´FR´=F1´+F2´+…+Fn´=平面力偶系可合成为一个力偶，这个力偶的矩Mo等于各附加力偶矩的代数和，又等于原来各力对点O的矩的代数和。n1iiFn1iiO)(MFoMOFR´(3—1)(3—2)F1F2oFnoFn´MnF1´M1F2´M24oF1F2oFnoFn´MnF1´M1F2´M2MOFR´取坐标系Oxy，i，j为沿x，y轴的单位矢量，则力系主矢的解析表达式为主矢FR´的大小和方向余弦为主矩的解析表达式22)∑()∑(yxFF'FR+='FF),'cos(RRxiF'FF),'cos(RRyjFyjxiRyRxRFF''+FF='F∑∑+=n1in1iiiiiiOO)F-F()(MMxyyxFxyijyxij5一物体的一端完全固定在另一物体上，这种约束称为固定端或插入端支座FAxFAyMAAAFAMA63.平面任意力系的简化结果分析简化结果可能有以下几种情况，即：（1）FR´=0，Mo≠0；（2）FR´≠0，Mo=0；（3）FR´≠0，Mo≠0；（4）FR´=0，Mo=0。FR´=0，Mo≠0原力系合成为合力偶，合力偶矩为（2）平面任意力系简化为一个合力的情形原力系简化为一个力，FR´就是原力系的合力,合力作用线通过简化中心O。n1iiOO)(MMF（1）平面任意力系简化为一个力偶的情形(a)FR´≠0，Mo=07oFR´Moo´oo´dFR´FR´´FRdoo´FR原力系简化为一个力，合力矢等于主矢；合力的作用线在点O的哪一侧，根据主矢和主矩的方向确定；合力作用线到点O的距离为d。'ROFMd平面任意力系平衡。（3）平面任意力系平衡的情形(b)FR´≠0，Mo≠0FR´=0，Mo=0FR´=FR=－FR´´8平面任意力系的合力矩定理由图(b),合力FR对点O的矩为由式（3—2）得合力矩定理：平面任意力系的合力对作用面内任一点的矩等于力系中各力对同一点的矩的代数和。n1i)(iOOMMFMO(FR)=FRd=MOn1i)()(iOROFMFM(b)oFR´Moo´oo´dFR´FR´´FRdoo´FR(c)(a)9例10已知F1=150N，F2=200N，F3=300N，F=F´=200N。求力系向点O的简化结果，并求力系合力的大小及其与原点O的距离。解：N437.652101cos45321FFFFxN161.651103sin45321FFFFyF31210020011F113F280FF´xyOjijiF161.6437.6′R10mN21.440.08510.2sin45.0.1)(31FFFFMMOO得力系向点O的简化结果如图（b);MOFR´Oxy(b)466.5N)161.6(437.6)()()(2222′yxRFFF466.5N′RRFF合力及其与原点O的距离如图(c)。mN21.44OM45.96mmROFMd(c)OxyFRdF31210020011F113F280FF´xyOji11例11水平梁AB受按三角形分布的载荷作用，如图示。载荷的最大值为q，梁长l，求合力作用线的位置。解:在梁上距A端为x处的载荷集度为q(x)=qx/l。在此处取的一微段dx，梁在微段dx受的力近似为F(x)=qxdx/l。2)(0lqdxxqFl设合力作用线到A端的距离为xC，llqlqxlxqFxlC3223d1202xdxq(x)dxlxxxqxF0cd)(FxcABlq梁由x=0到x=l的分布载荷合力为根据合力矩定理12小结1.力的平移定理:平移一力的同时必须附加一个力偶，附加力偶的矩等于原来的力对新作用点的矩。2.平面任意力系向平面内任选一点O简化:可得一个力和一个力偶。这个力等于该力系的主矢，作用线通过简化中心O。这个力偶的矩等于该力系的主矩。jFiFFFyxiR'3.平面任意力系的简化结果...