§1.2.4(1)绝对值VIP免费

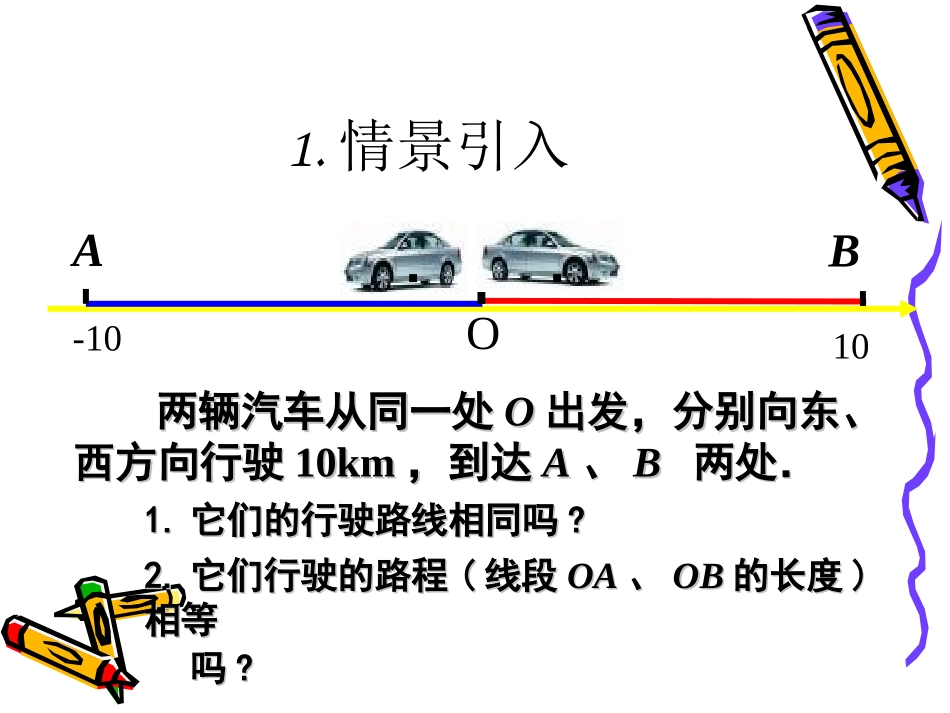
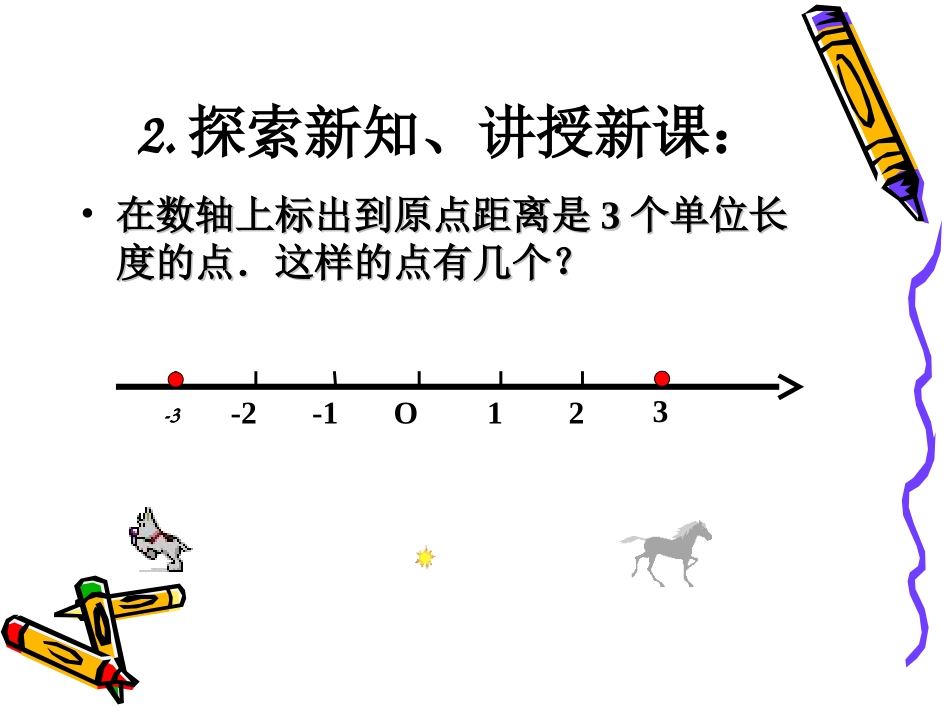
1.2.41.2.4绝对值绝对值((第第11课时课时))1.2.41.2.4绝对值绝对值((第第11课时课时))濯港镇第一初级中学-10两辆汽车从同一处两辆汽车从同一处OO出发，分别向东、出发，分别向东、西方向行驶西方向行驶10km10km，到达，到达AA、、BB两处．两处．2.2.它们行驶的路程它们行驶的路程((线段线段OAOA、、OBOB的长度的长度))相等相等吗吗??1.1.它们的行驶路线相同吗它们的行驶路线相同吗??O10AB··1.情景引入2.探索新知、讲授新课：•在数轴上标出到原点距离是在数轴上标出到原点距离是33个单位长个单位长度的点．这样的点有几个？度的点．这样的点有几个？O1-1-223-3│-4│=410-1-2-3-4432-554数轴上表示数数轴上表示数aa的点与原点的距离叫做的点与原点的距离叫做数数aa的的绝对值绝对值..用用|a||a|表示表示..（（aa可以取所有的正数、负数和可以取所有的正数、负数和00．）．）定义定义例题讲解•(1)|+8|=,||=,|+10.6|=.•(2)|0|=.•(3)|-12|=,∣-1.6∣=,=.151513278810.610.600121.61327问问::一个数的绝对值与这个数一个数的绝对值与这个数有什么关系？有什么关系？问问::一个数的绝对值与这个数有一个数的绝对值与这个数有什么关系？什么关系？•绝对值的代数意义绝对值的代数意义：：(1)(1)正数的绝对值是正数的绝对值是它本身；它本身；(2)0(2)0的绝对值是的绝对值是00．．(3)(3)负数的绝对值是它负数的绝对值是它的相反数；的相反数；,0,0,0aaaaa0a思考•(1)(1)任何一个有理数都有绝对值吗？一个数的绝任何一个有理数都有绝对值吗？一个数的绝对值有几个对值有几个??–----------任何有理数都有唯一的绝对值任何有理数都有唯一的绝对值•(2)(2)有没有绝对值是有没有绝对值是-2-2的数的数??•------任意一个数的绝对值总是正数或任意一个数的绝对值总是正数或00，不可能，不可能是负数是负数•(3)(3)互为相反数的两数绝对值有什么关系？互为相反数的两数绝对值有什么关系？•--------相等相等•（（44）绝对值等于它本身的是什么数呢？）绝对值等于它本身的是什么数呢？•--------非负数非负数例1.求下列各数的绝对值：151,,4.75,10.5.210解：151522||111010|||-4.75|=4.75|10.5|=10.5例2.化简：1(1)|()|;21(2)|1|.3111(1)|()|||.22211(2)|1|133解：巩固练习巩固练习11：：•1．课本第课本第1212页练习页练习11，，22•2．计算：计算：13(1)(2);(2)1;(3)43;24556(4)210;(5)(4.2);(6).765（7）|8|+||8|+|－－8|8|－－||－－3|3|．．(8)|3.14-|=(8)|3.14-|=..3.141.数轴上与原点的距离小于5,且表示整数的点有()个;2.绝对值小于3.5的整数有()个.它们（）99770,0,土土1,1,土土2,2,土土330-5+5课堂练习二课堂练习二3.绝对值大于2且不大于5的整数有()个,其中最大的是(),最小的是().6655-5-50-5+52-22<|x|≤54.4.若若aa＜＜0,│5a│=0,│5a│=（）（）5.5.若若aa＞＞2,│a-2│=()2,│a-2│=()6.6.若若aa＞＞4,│4-a│=()4,│4-a│=()-5a-5aa-2a-2a-4a-43．利用数轴回答一下问题利用数轴回答一下问题•（11）绝对值小于）绝对值小于44的整数有的整数有..•（（22）绝对值大于）绝对值大于22而小于而小于55的所有整数是的所有整数是..•（（33）如果）如果,,那么那么aa和和bb的关系的关系是是..•（（44）如果一个数的绝对值是）如果一个数的绝对值是1313，那么这个数，那么这个数是是..-3,-2,-1,-3,-2,-1,0,1,2,30,1,2,33,43,4aba=ba=b或或a=-ba=-b1313或－或－1313•44．求绝对值小于．求绝对值小于33的所有整数和的所有整数和．．•55．如果．如果求：求：aa、、bb的值．的值．•6.6.如果，如果，求：求：a-3ba-3b的值．的值．3280ab0562ba课堂小结：课堂小结：11．．概念：概念：一个数的绝对值是在数轴上表示这个数的点到原点的一个数的绝对值是在数轴上表示这个数的点到原点的距离距离．．２．（非负性）２．（非负性）３．３．代数意义：代数意义：正数的绝对值是它本身，负数的绝对值是它的相正数的绝对值是它本身，负数的绝对值是它的相反数，反数，0...