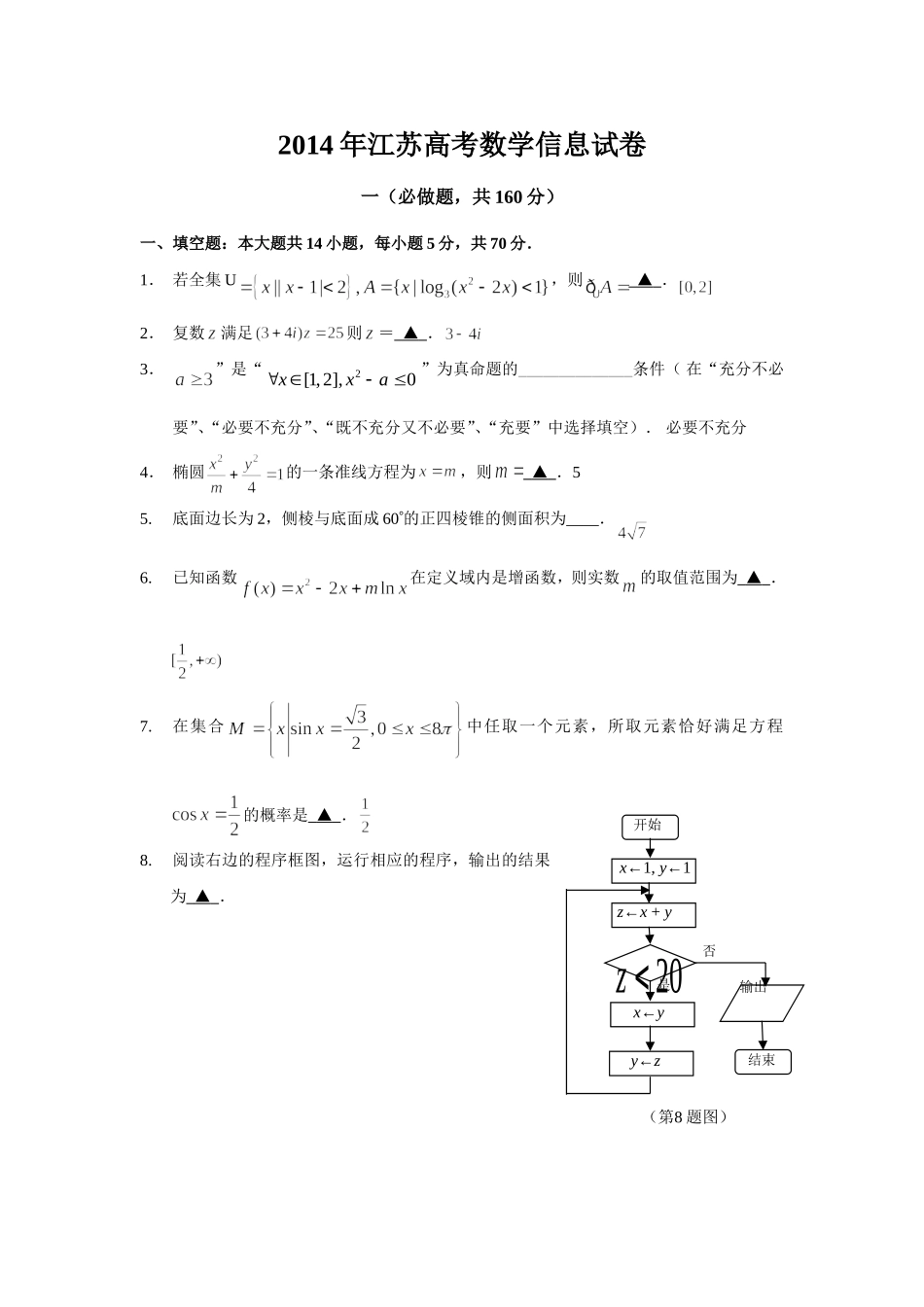
输出开始结束20z是否(第8题图)x←1,y←1z←x+yx←yy←z2014年江苏高考数学信息试卷一(必做题,共160分)一、填空题:本大题共14小题,每小题5分,共70分.1.若全集U,则▲.2.复数满足则=▲.3.”是“2[1,2],0xxa”为真命题的______________条件(在“充分不必要”、“必要不充分”、“既不充分又不必要”、“充要”中选择填空).必要不充分4.椭圆的一条准线方程为,则▲.55.底面边长为2,侧棱与底面成60的正四棱锥的侧面积为____.6.已知函数在定义域内是增函数,则实数的取值范围为▲.7.在集合中任取一个元素,所取元素恰好满足方程的概率是▲.8.阅读右边的程序框图,运行相应的程序,输出的结果为▲.9.已知,是空间中两条不同的直线,,,是空间中三个不同的平面,则下列命题正确的序号是▲.①若,,则;②若,,则;③若,,则;④若,,则.10.在等差数列中,前2m(m为正整数)和为155,其中奇数项的和为70,且,该数列的通项公式为▲.11.两非零向量,的夹角为,向量,(其中),当最小时,与夹角的大小为▲.12.设圆,过圆心作直线交圆于两点,并与轴交于点,若点恰好为的中点,则直线的方程为.或13.已知函数,若对于任意,都有,其中为正常数,则可取到的最小值为▲.14.集合其中,对应图形的面积为▲.答案:15.(本题满分14分)已知三角形顶点的坐标分别为.(1)求的坐标;(2)若边的中点为,求的值;(3)若点是三角形的外心,求的值.说明:本题主要考查了坐标下向量的加法、减法、数量积等基本运算,属容易题.解:(1),4分(2)边的中点6分10分(3).12分14分16.(本题满分14分)如图,正六棱锥底边边长为2,高为.设平面与平面交于直线.求证:(1)//;(2)面面.(1)证明://,面,面,3分//面.又面面,且//.6分(2)设面于,取的中点分别是,连结,则,且,PBFCDEAOHGl由已知得,,从而.9分又面,,从而面,又,所以.12分又,所以,又,所以面面.14分17.一个如图所示的不规则形铁片,其缺口边界是口宽4分米,深2分米(顶点至两端点所在直线的距离)的抛物线形的一部分,现要将其缺口边界裁剪为等腰梯形.(1)若保持其缺口宽度不变,求裁剪后梯形缺口面积的最小值;(2)若保持其缺口深度不变,求裁剪后梯形缺口面积的最小值.解:(1)以抛物线顶点为原点,对称轴为轴,建立平面直角坐标系,则,从而边界曲线的方程为,.……4分因为抛物线在点处的切线斜率,所以,切线方程为,与轴的交点为.此时梯形的面积平方分米,即为所求.……7分(2)设梯形腰所在直线与抛物线切于时面积最小.此时,切线方程为,其与直线相交于,与轴相交于.……10分yABCDO此时,梯形的面积,.……11分(这儿也可以用基本不等式,但是必须交代等号成立的条件)=0,得,当时,单调递减;当时,单调递增,故,当时,面积有最小值为.……14分18(本题满分16分)如图,在直角坐标系中,为直角坐标系的原点,椭圆:过点,且椭圆的离心率为,已知椭圆的内接四边形(逆时针排列)的对角线均过坐标原点,且,(1)求椭圆的方程;(2)求证:为定值,并求出这个定值.解:(1)椭圆中,,①又,3分代入①解得:.椭圆的方程为:.6分(2)由于点与、与关于原点对称,故,从而,,设直线的斜率为,则,代入椭圆的方程得:,,9分用,可得:,12分又当或不存在时,分别是椭圆的长半轴、短半轴的长(可交换),综上所述:均为定值.16分19(本题满分16分)设,.(1)若恒成立,求实数的取值范围;(2)当时,解不等式;(3)若时,恒成立,求实数的取值范围.说明:第(1)(2)小题考查了二次函数的性质、一元二次不等式的解法及分类讨论的基本数学思想,属容易题;第(3)小题以不等式恒成立、函数值域的求法等综合性问题为载体,主要考查了学生观察、判断能力及等价转化能力,属中档题.解:(1)恒成立2分.4分(2),1)当时,,原不等式解为一切实数;2)当时,原不等式解为:.3)当时,,原不等式的解为:.8分(3)令它在(1,2)上是增函数,故,从而当时,恒成立即对于恒成立,;因为当时,,所以,12分,所以函数在(3,8)上是减函数.,从而.16...