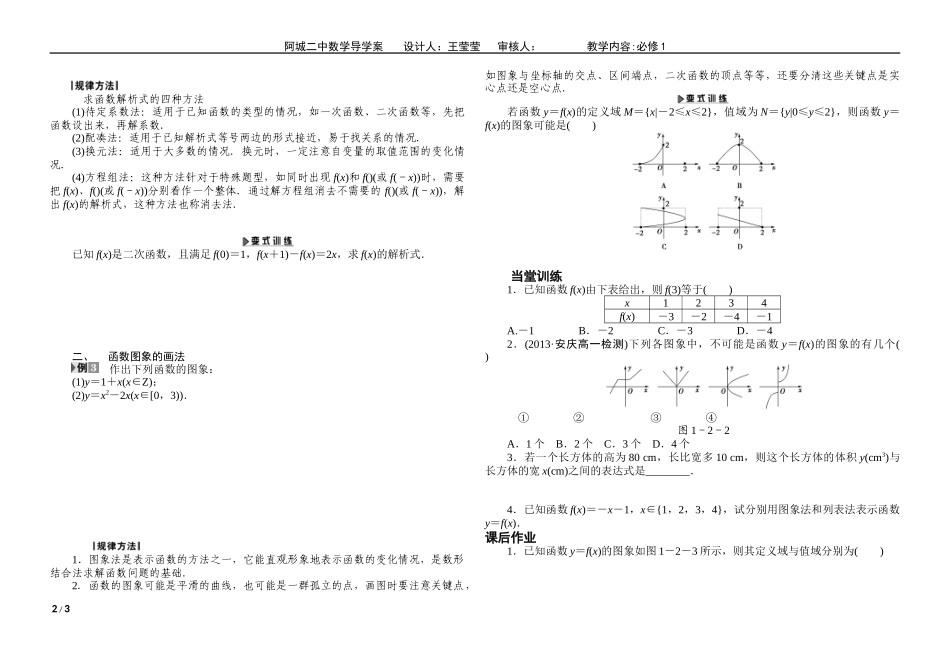
阿城二中数学导学案设计人:王莹莹审核人:教学内容:必修11.2.2函数的表示法(1)第1课时函数的表示法课标解读1.掌握函数的三种表示方法:解析法、图象法、列表法.(重点)2.会根据不同的需要选择恰当方法表示函数.(难点)课前预习一、函数的表示法【问题导思】函数有哪几种常用的表示法?列表法、图象法和解析法.课上探究一、函数的三种表示法某商场新进了10台彩电,每台售价3000元,试求售出台数x与收款数y之间的函数关系,分别用列表法、图象法、解析法表示出来.1.本题中函数的定义域是不连续的,作图时应注意函数图象是一些点,而不是直线.另外,函数的解析式应标明定义域.2.解析法、图象法和列表法分别从三个不同的角度刻画了自变量和函数值的对应关系.已知函数f(x),g(x)分别由下表给出:x123f(x)211x123g(x)321则f(g(1))的值为________;当g(f(x))=2时,x=________.二、求函数的解析式(1)已知f(x)是一次函数且f(f(x))=2x-1,则f(x)=________.(2)已知函数f(x)对于任意的x都有f(x)+2f(-x)=3x-2,则f(x)的解析式为________.(3)已知f(+1)=x+2,求f(x)的解析式.1/3阿城二中数学导学案设计人:王莹莹审核人:教学内容:必修1求函数解析式的四种方法(1)待定系数法:适用于已知函数的类型的情况,如一次函数、二次函数等,先把函数设出来,再解系数.(2)配凑法:适用于已知解析式等号两边的形式接近,易于找关系的情况.(3)换元法:适用于大多数的情况.换元时,一定注意自变量的取值范围的变化情况.(4)方程组法:这种方法针对于特殊题型,如同时出现f(x)和f()(或f(-x))时,需要把f(x)、f()(或f(-x))分别看作一个整体.通过解方程组消去不需要的f()(或f(-x)),解出f(x)的解析式,这种方法也称消去法.已知f(x)是二次函数,且满足f(0)=1,f(x+1)-f(x)=2x,求f(x)的解析式.二、函数图象的画法作出下列函数的图象:(1)y=1+x(x∈Z);(2)y=x2-2x(x∈[0,3)).1.图象法是表示函数的方法之一,它能直观形象地表示函数的变化情况,是数形结合法求解函数问题的基础.2.函数的图象可能是平滑的曲线,也可能是一群孤立的点,画图时要注意关键点,如图象与坐标轴的交点、区间端点,二次函数的顶点等等,还要分清这些关键点是实心点还是空心点.若函数y=f(x)的定义域M={x|-2≤x≤2},值域为N={y|0≤y≤2},则函数y=f(x)的图象可能是()当堂训练1.已知函数f(x)由下表给出,则f(3)等于()x1234f(x)-3-2-4-1A.-1B.-2C.-3D.-42.(2013·安庆高一检测)下列各图象中,不可能是函数y=f(x)的图象的有几个()①②③④图1-2-2A.1个B.2个C.3个D.4个3.若一个长方体的高为80cm,长比宽多10cm,则这个长方体的体积y(cm3)与长方体的宽x(cm)之间的表达式是________.4.已知函数f(x)=-x-1,x∈{1,2,3,4},试分别用图象法和列表法表示函数y=f(x).课后作业1.已知函数y=f(x)的图象如图1-2-3所示,则其定义域与值域分别为()2/3阿城二中数学导学案设计人:王莹莹审核人:教学内容:必修1图1-2-3A.[-3,3),[-2,2]B.[-3,-1)∪(-1,3],[-2,2]C.[-3,-1)∪(-1,3),(-2,2]D.(-3,3],[-2,2)2.已知f(x+2)=x2-x+1,则f(x)等于()A.x2-x+3B.x2+4x+1C.x2-x-1D.x2-5x+73.已知函数f(x-1)=x2-3,则f(2)的值为()A.-2B.6C.1D.04.如果二次函数的图象开口向上且关于直线x=1对称,且过点(0,0),则此二次函数的解析式可以是()A.f(x)=x2-1B.f(x)=-(x-1)2+1C.f(x)=(x-1)2+1D.f(x)=(x-1)2-15.(2013·安阳高一检测)下列所给4个图象中,与所给3件事吻合最好的顺序为()(1)我离开家不久,发现自己把作业本忘在家里了,于是立刻返回家里取了作业本再上学;(2)我骑着车一路以常速行驶,只是在途中遇到一次交通堵塞,耽搁了一些时间;(3)我出发后,心情轻松,缓缓行进,后来为了赶时间开始加速.(1)(2)(3)(4)图1-2-4A.(1)(2)(4)B.(4)(2)(3)C.(4)(1)(3)D.(4)(1)(2)6.函数f(x)的图象如图1-2-5所示,其中点O、A、B、C的坐标分别为(0,0),(-5,),(0,4),(2,0),则f(-5)=________,f(f(...