职高数学7.1.4平面向量数乘VIP免费

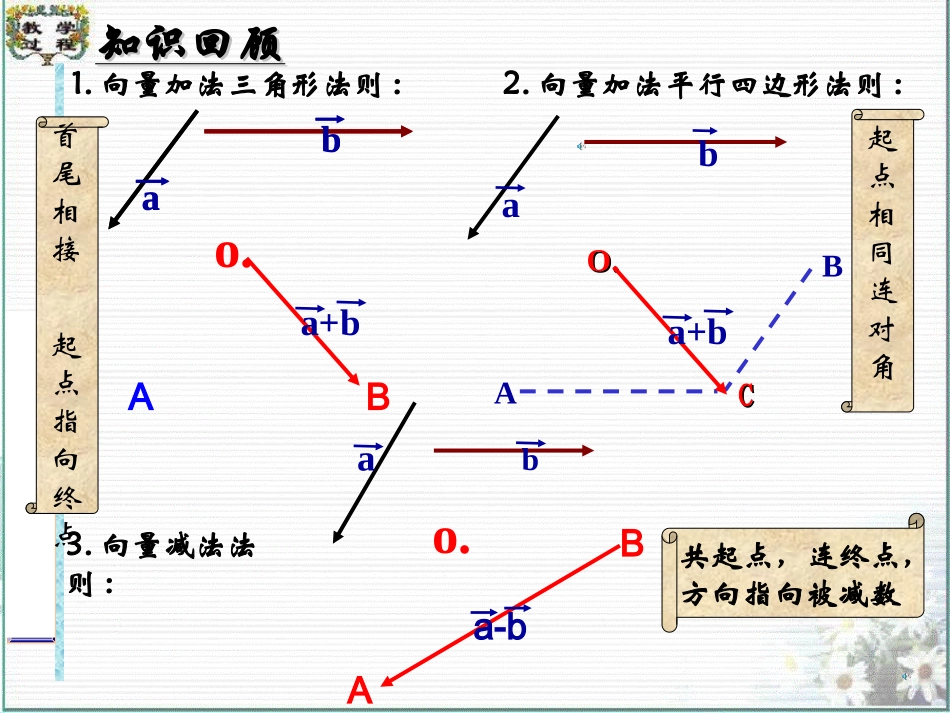
7.1.47.1.4向量数乘运算向量数乘运算及其几何意义及其几何意义下页上页首页小结结束知识回顾知识回顾BAbao.OO..CCa+bbaABba+ba1.向量加法三角形法则:2.向量加法平行四边形法则:首尾相接起点指向终点起点相同连对角o.BAa-bab3.向量减法法则:共起点，连终点，方向指向被减数思考：已知非零向量，作出和，你能说明它们的几何意义吗？aaaa()()()aaaaOaaaABC3aPQaMaNa3a3a与a方向相同|3a|=3|a|-3a与a方向相反|-3a|=3|a|下页上页首页小结结束一、向量的数乘定义一、向量的数乘定义(1)(1)长度长度(2)(2)方向方向特别的，当时，00.a一般地，我们规定实数λ与向量的积是一个向量，这种运算叫做向量的数乘，记作，它的长度和方向规定如下：||||||;aa当时，的方向与的方向相同；当时，的方向与的方向相反。0aaaa0aa下页上页首页小结结束二、向量数乘的几何意义a-3aa213aa21a几何意义：将的长度扩大（或缩小）倍，改变几何意义：将的长度扩大（或缩小）倍，改变（或不改变）的方向，就得到了（或不改变）的方向，就得到了λλaa|λ||λ|aaaa下页上页首页小结结束结论:2a+2b=2(a+b)结论:3(2a)=6a(1)(1)根据定义，求作向量根据定义，求作向量3(2a)3(2a)和和(6a)(a(6a)(a≠0≠0))，并比较。，并比较。abbaba22a2b2(2)(2)已知向量已知向量a,ba,b，求作向量，求作向量2(a+b)2(a+b)和和2a+2b2a+2b，并比较。，并比较。a)2(3a)2(3aa6=观察总结观察总结()()aa()abab(3)(3)根据定义，求作向量根据定义，求作向量(2+3)(2+3)aa和和22aa+3a+3a((aa为非零向量为非零向量))，并进行比较。，并进行比较。a5a2a3a(23)23aaa()aaa下页上页首页小结结束①①λ(μa)=λ(μa)=运算运算律律::设设aa、、bb为任意向量，为任意向量，λλ、、μμ为任意实数，则为任意实数，则有：有：②②(λ+μ)a=(λ+μ)a=③③λ(a+b)=λ(a+b)=(λμ)a(λμ)aλa+μaλa+μaλa+λbλa+λb（（-λ-λ））a=-(a=-(λa)=λ(-a)λa)=λ(-a)特别地，λ(a-b)=λ(a-b)=λλa-λba-λb结合律结合律第一分配律第一分配律第二分配律第二分配律三、向量数乘运算满足的运算律：下页上页首页小结结束解解:(1):(1)原式原式==(2)(2)原式原式==(3)(3)原式原式==计算：计算：((口答口答))(1)(-3)×4a(1)(-3)×4a(2)3(a+b)(2)3(a+b)––2(a-b)-a2(a-b)-a(3)(2a+3b-c)(3)(2a+3b-c)––(3a-2b+c)(3a-2b+c)(3-2-1)a+(3+2)b(3-2-1)a+(3+2)b=5b=5b(2-3)a+(3+2)b+(-1-1)c(2-3)a+(3+2)b+(-1-1)c=-a+5b-2c=-a+5b-2c-12a-12a牛刀小试牛刀小试结论：向量的加、减、数乘运算统称为向量的加、减、数乘运算统称为向量的线性运算。向量的线性运算。练习：练习：7.1.47.1.4下页上页首页小结结束(1)3,6(2)8,1421(3),3332(4),43aebeaebeaebeaebe2ba74ba例1：把下列各小题中的向量b表示为实数与向量a的积.a21ba98b