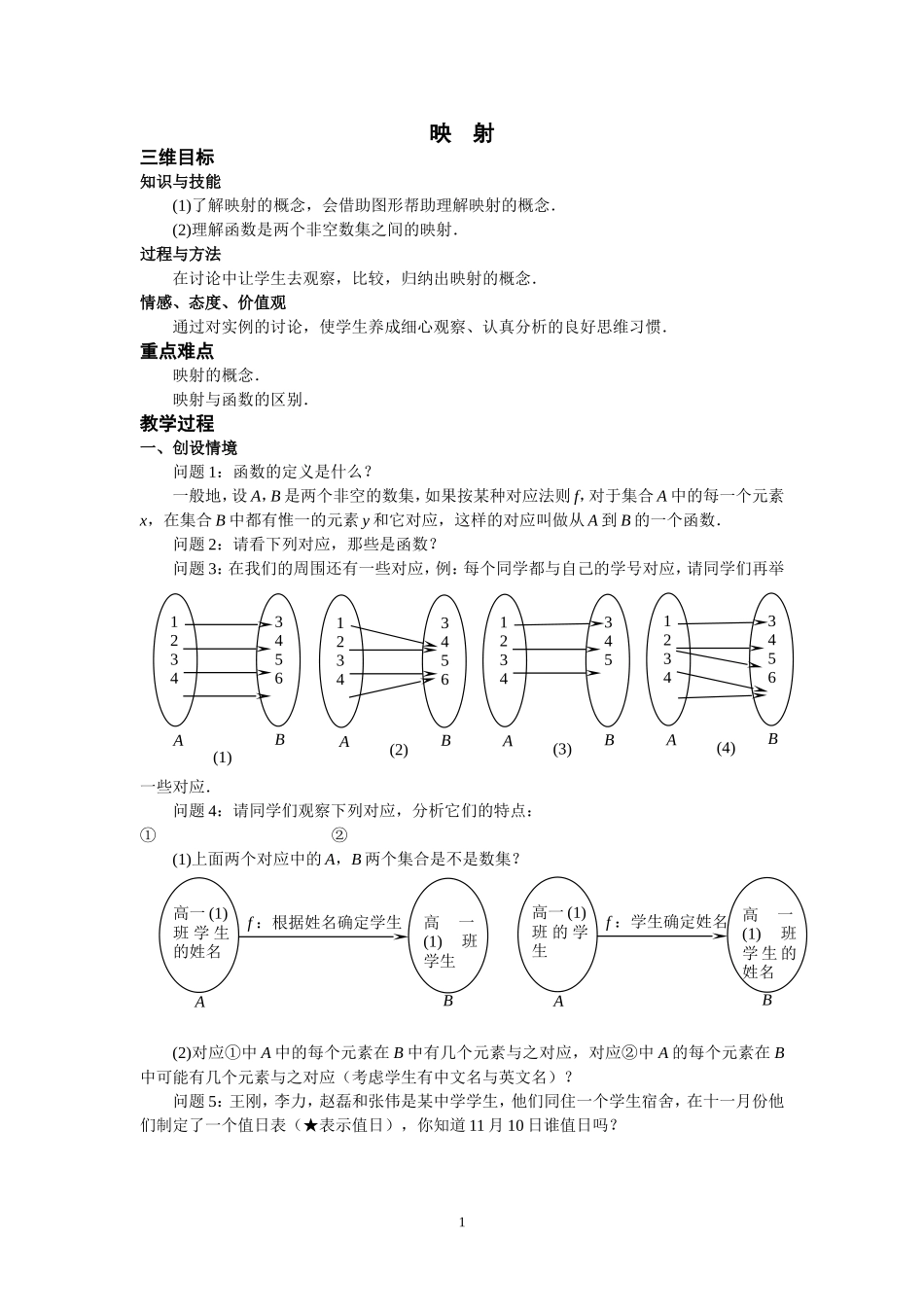
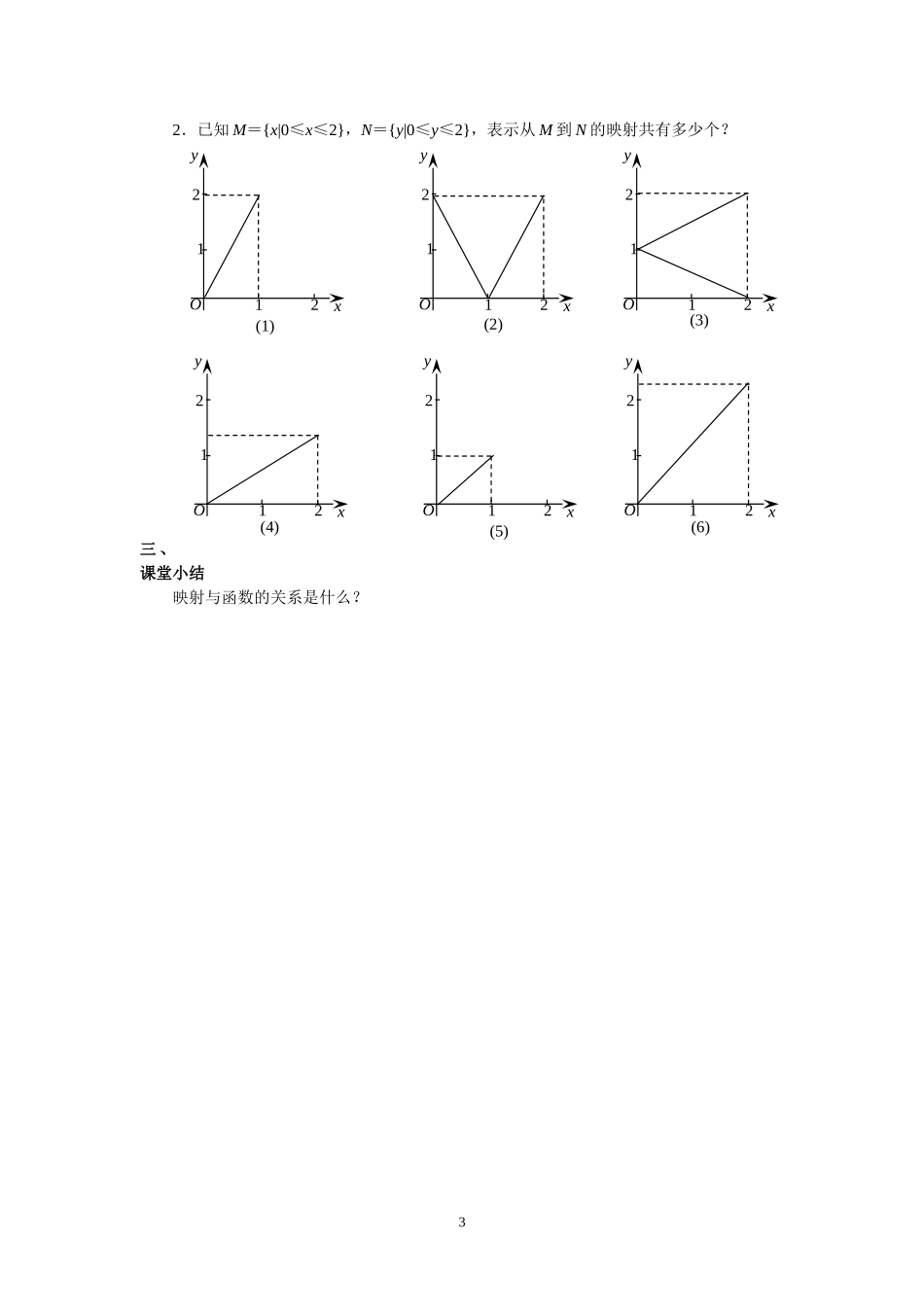
映射三维目标知识与技能(1)了解映射的概念,会借助图形帮助理解映射的概念.(2)理解函数是两个非空数集之间的映射.过程与方法在讨论中让学生去观察,比较,归纳出映射的概念.情感、态度、价值观通过对实例的讨论,使学生养成细心观察、认真分析的良好思维习惯.重点难点映射的概念.映射与函数的区别.教学过程一、创设情境问题1:函数的定义是什么?一般地,设A,B是两个非空的数集,如果按某种对应法则f,对于集合A中的每一个元素x,在集合B中都有惟一的元素y和它对应,这样的对应叫做从A到B的一个函数.问题2:请看下列对应,那些是函数?问题3:在我们的周围还有一些对应,例:每个同学都与自己的学号对应,请同学们再举一些对应.问题4:请同学们观察下列对应,分析它们的特点:①②(1)上面两个对应中的A,B两个集合是不是数集?(2)对应①中A中的每个元素在B中有几个元素与之对应,对应②中A的每个元素在B中可能有几个元素与之对应(考虑学生有中文名与英文名)?问题5:王刚,李力,赵磊和张伟是某中学学生,他们同住一个学生宿舍,在十一月份他们制定了一个值日表(★表示值日),你知道11月10日谁值日吗?112343456AB(1)12343456AB(2)1234345AB(3)12343456AB(4)高一(1)班学生高一(1)班学生的姓名f:根据姓名确定学生AB高一(1)班学生的姓名高一(1)班的学生f:学生确定姓名AB日期12345678…30王刚★★…李力★★…★赵磊★★…张伟★★…二、讲解新课数学理论:一般地,设A,B是两个的集合,如果按某种对应法则f,对于集合A中的每一个元素x,在集合B中都有惟一的元素y和它对应,这样的单值对应叫做从集合A到集合B的映射,记作:f:A→B.说明:(1)映射是函数概念的推广,函数是一类特殊的映射;(2)对于映射f:AB而言,集合A、B可以是数集,也可以是点集或其他集合;(3)映射的方向性:映射f:AB与f:BA是不一样的.例题讲解:例1(1)A=Z,B=N*,对应法则f:x→|x|是不是A到B的映射?为什么?(2)A={11,16,20,21},B={6,2,4,0,1},对应法则f:求被7除的余数,说明f是A到B的映射.解:(1)对应法则f:x→|x|不是A到B的映射,因为集合A中的元素0在集合B中没有元素与之对应,所以不是映射.(2)因为按照对应法则f,集合A中的元素11与4对应,16与2对应,20与6对应,21与0对应,即集合A中的每一个元素按照对应法则f在集合B中都有唯一的元素与之对应,所以f是A到B的映射.例2请分析下列对应,哪些是A到B的映射?(1)A=R,B={x|x是数轴上的点},f:实数与数轴上的点对应;(2)A={中国,日本,韩国},B={北京,东京,汉城,华盛顿},f:相应国家的首都;(3)A={x|x是金陵中学高一年级有QQ号的学生},B={x|x是QQ号码},f:该生对应的QQ号;(4)A={x|x是高一年级的班级},B={x|x是金陵中学高一年级的学生},f:该班级对应的学生.解:由于实数与数轴上的点是一一对应的,所以(1)是映射;因为中国的首都是北京,日本的首都是东京,韩国的首都是汉城,所以(2)是映射;因为每一个有QQ号的学生不一定只有一个QQ号,所以(3)不是映射;因为一个班级里不止一个学生,所以(4)不是映射.说明:映射可以是“一对一”或“多对一”的对应,但不能是“一对多”.课堂训练:1.在下列从A到B的对应中,是映射的有()(1)A=R,B=R,对应法则f:x→y=(2)A=R,B=R,对应法则f:x→y=(3)A=(0,+∞),B={y|y≠0}对应法则f:x→y=(4)A=N*,B={-1,1}对应法则f:x→y=(-1)nA.(1)(3)B.(3)(4)C.(1)(4)D.(2)(3)22.已知M={x|0≤x≤2},N={y|0≤y≤2},表示从M到N的映射共有多少个?三、课堂小结映射与函数的关系是什么?3yxO1122(1)yxO1122(2)yxO1122(3)yxO1122(4)yxO1122(5)yxO1122(6)