课时14：一次函数VIP免费

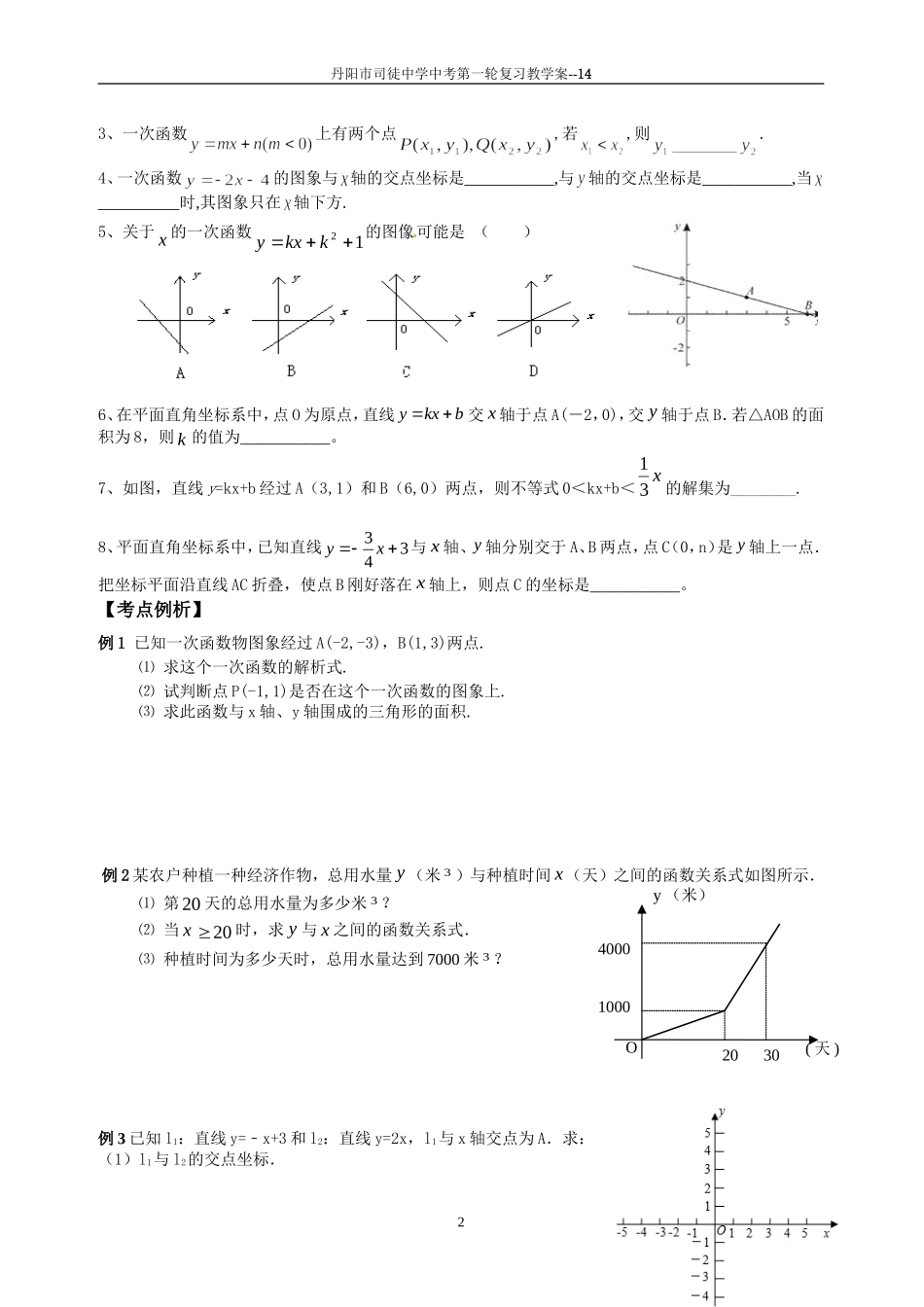
丹阳市司徒中学中考第一轮复习教学案--14课时14：一次函数【学习目标】1．结合具体情境体会一次函数的意义，能根据已知条件确定一次函数的解析式．2．经历列表、描点、连线画一次函数图象的过程，根据一次函数的图象和解析式y＝kx＋b(k≠0)，探索并理解k>0和k<0时图象的变化情况，弄能灵活运用．3．理解正比例函数，掌握正比例函数的图象和性质并能灵活运用．4．会利用待定系数法确定正比例函数和一次函数的解析式．5．会用函数图象的方法求方程（组）与不等式（组）的解（集）．【知识梳理】1．正比例函数的一般形式是__________．一次函数的一般形式是__________________.2.一次函数的图象与坐标轴交点坐标为__________________________.3.一次函数的图象与性质4．用待定系数法求一次函数关系式的一般步骤：(1)设出函数关系式为________．(2)找到两个已知点的坐标，并代入所设函数关系式得到关于k、b的方程组．[来源:Z。xx。k.Com](3)解方程组求出k、b的值．(4)把得到的k、b的值代入所设关系式．5．由于任何一元一次方程都可以化为ax＋b＝0（a、b为常数，a≠0）的形式，所以解一元一次方程可以转化为：当一次函数y＝ax＋b的值为0时，求相应的自变量的值，从图象上看，这相当于已知直线y＝ax＋b，确定它与_______交点的横坐标的值．6．由于任何一元一次不等式都可以化为ax＋b>0或ax＋b<0(a、b为常数，a≠0)的形式，所以解一元一次不等式可以看作：当一次函数y＝ax＋b的值大（小）于0时，求自变量相应的_______．7．一般地，每个二元一次方程组都对应两个一次函数，于是也对应两条直线．从“数”的角度看，解方程组相当于考虑自变量为何值时两个函数的值_______以及这个函数值为何值；从“形”的角度看，解方程组相当于确定两条直线交点的坐标。【知识应用】1、若函数28(3)mymx-=-是正比例函数，则常数m的值是。2、已知关于x的一次函数24kkxy0k。若其图像经过原点，k，若y随着x的增大而减小，则k的取值范围是。k、b的符号k＞0b＞0k＞0b＜0k＜0b＞0k＜0b＜0画出图像的大致位置经过象限性质y随x的增大而y随x的增大而y随x的增大而y随x的增大而1丹阳市司徒中学中考第一轮复习教学案--143、一次函数上有两个点,若,则.4、一次函数的图象与轴的交点坐标是___________,与轴的交点坐标是___________,当__________时,其图象只在轴下方.5、关于x的一次函数12kkxy的图像可能是（）6、在平面直角坐标系中，点O为原点，直线ykxb交x轴于点A(－2，0)，交y轴于点B．若△AOB的面积为8，则k的值为___________。7、如图，直线y=kx+b经过A（3,1）和B（6,0）两点，则不等式0＜kx+b＜x31的解集为________.8、平面直角坐标系中，已知直线334yx与x轴、y轴分别交于A、B两点，点C（0，n）是y轴上一点．把坐标平面沿直线AC折叠，使点B刚好落在x轴上，则点C的坐标是___________。【考点例析】例1已知一次函数物图象经过A(-2,-3)，B(1,3)两点.⑴求这个一次函数的解析式.⑵试判断点P(-1,1)是否在这个一次函数的图象上.⑶求此函数与x轴、y轴围成的三角形的面积.例2某农户种植一种经济作物，总用水量y（米3）与种植时间x（天）之间的函数关系式如图所示．⑴第20天的总用水量为多少米3？⑵当x20时，求y与x之间的函数关系式．⑶种植时间为多少天时，总用水量达到7000米3？例3已知l1：直线y=﹣x+3和l2：直线y=2x，l1与x轴交点为A．求：（1）l1与l2的交点坐标．2O(天)y（米）400010003020xyO32yxa1ykxb丹阳市司徒中学中考第一轮复习教学案--14（2）经过点A且平行于l2的直线的解析式．【质疑反馈】1.直线y＝2x＋b经过点(1，3)，则b＝_________．2.已知直线y＝2x＋8与x轴和y轴的交点的坐标分别是_______、_______；与两条坐标轴围成的三角形的面积是__________．3.如果直线经过第一、二、三象限,那么____0．(填“>”、“<”、“=”)4．如图，将直线OA向上平移1个单位，得到一个一次函数的图像，那么这个一次函数的解析式是．5.下列各点中，在函数的图象上的是（）A．（2，3）B．（3，1）C．（0，－7）D．（－1，9）6.直线与轴的交点是(1，0)，则的值是()A.3B.2C.－2D.－37.一次函...