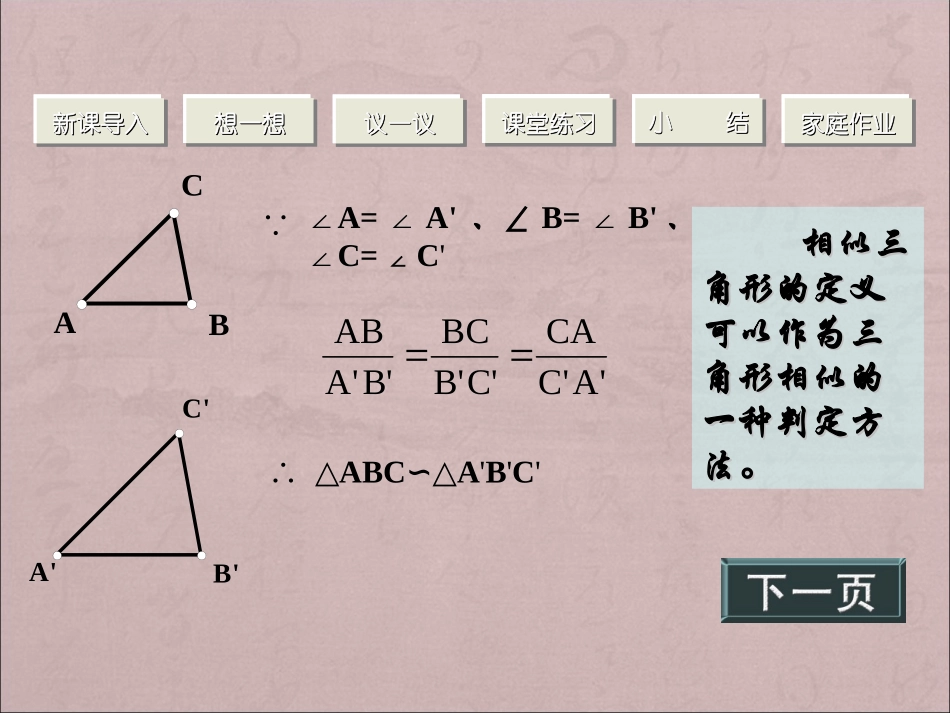
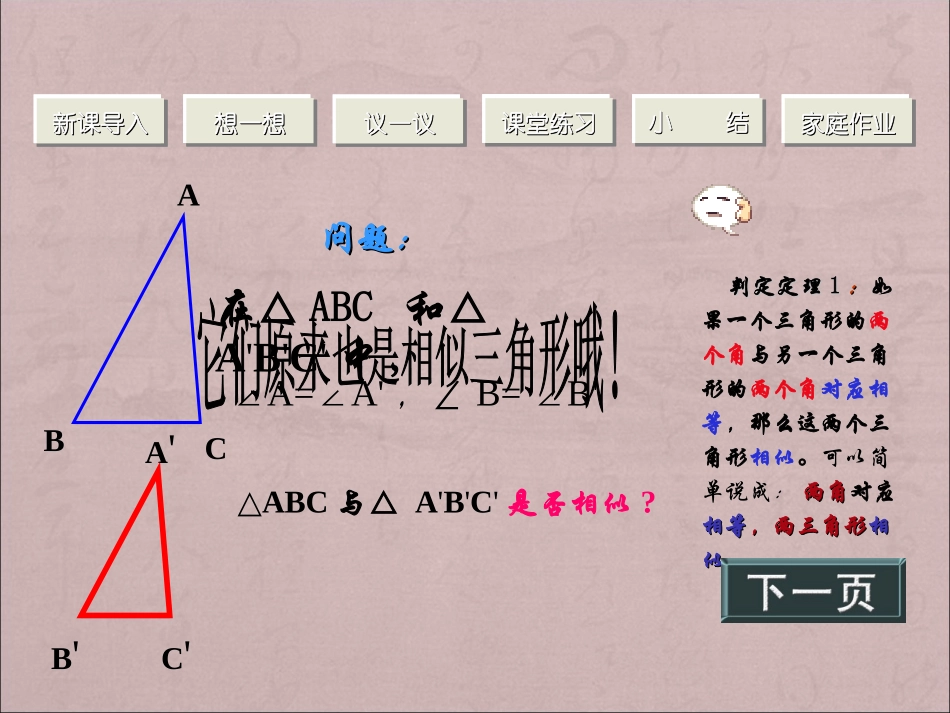
第4节探索三角形相似的条件(一)CBAC'B'A'∵∠A=A'∠、∠B=B'∠、∠C=∠C''A'CCA'C'BBC'B'AAB∴△ABCA∽△'B'C'相似三相似三角形的定义角形的定义可以作为三可以作为三角形相似的角形相似的一种判定方一种判定方法。法。新课导入新课导入新课导入新课导入想一想想一想想一想想一想议一议议一议议一议议一议课堂练习课堂练习课堂练习课堂练习小小结结小小结结家庭作业家庭作业家庭作业家庭作业ABCA'C'B'问题:问题:在△ABC和△A'B'C'中,∠A=A'∠,∠B=B'∠△ABC与△A'B'C'是否相似?判定定理判定定理11::如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。可以简单说成:两角两角对应相等相等,两三角形,两三角形相相似似。。新课导入新课导入新课导入新课导入想一想想一想想一想想一想议一议议一议议一议议一议课堂练习课堂练习课堂练习课堂练习小小结结小小结结家庭作业家庭作业家庭作业家庭作业用数学符号表示:用数学符号表示:ABCA'C'B'∵∠A=A∠',∠B=B∠'∴ΔABCΔA∽'B'C'咦?是咦?是这么表示这么表示的?的?新课导入新课导入新课导入新课导入想一想想一想想一想想一想议一议议一议议一议议一议课堂练习课堂练习课堂练习课堂练习小小结结小小结结家庭作业家庭作业家庭作业家庭作业练习练习11::ΔABC和ΔDEF中,∠A=40°,∠B=80°,∠E=80°,∠F=60°。ΔABC与ΔDEF(“相似”或“不相似”)。??ACB40°80°FED80°60°相似动动手啊新课导入新课导入新课导入新课导入想一想想一想想一想想一想议一议议一议议一议议一议课堂练习课堂练习课堂练习课堂练习小小结结小小结结家庭作业家庭作业家庭作业家庭作业练习练习22有一个锐角相等的两直角三角形是否为相似三角形?动动手啊新课导入新课导入新课导入新课导入想一想想一想想一想想一想议一议议一议议一议议一议课堂练习课堂练习课堂练习课堂练习小小结结小小结结家庭作业家庭作业家庭作业家庭作业3已知等腰三角形ΔABC和ΔA/B/C/中,∠A、∠A/分别是顶角,求证:①如果∠A=A∠/,那么ΔABCΔA∽/B/C/。②如果∠B=B∠/,那么ΔABCΔA∽/B/C/。A/ABCB/C/BCB/C/AA/4.有一对角相等的等腰三角形是相似三角形。这句话正确吗?ABCA′′CB′55、、已知已知:在△:在△ABCABC与与△△DEFDEF中,中,∠∠AA==48°48°,,∠∠BB==82°82°,∠,∠DD==48°48°,∠,∠FF==50°50°求证:△ABC∽△DEF。证明:在△DEF中,∠E=180°-∠D-∠F=180°-48°-50°=82°∵∠A=∠D=48°,∠B=∠E=82°∴△ABC∽△DEF(两角对应相等的两个三角形相似)6、在一次数学活动课上,为了测量河宽AB,小明采用了如下的方法(如图)从A处沿与AB垂直的直线方向走40米到达C处,插一根标竿,然后沿同方向继续走15米到达D处,再向右转90度走到E处,使B、C、E三点恰好在一条直线上,量得DE=20米,这样就可以求出河宽AB,请你算出结果(要求写出解题过程)。ABDCE方法一ABO方法二ED7、已知:如图,在△ABC中,DE∥BC求证:△ADE∽△ABCAECBDADEBC2图()ABCED3图()推论:平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似。1、用数学符号表述:条件:∠A=∠D,∠B=∠E结论:△ABC∽△DEF2、用几何语言表述:如果一个三角形的两角分别与另一个三角形的两角对应相等,那么这两个三角形相似。两角对应相等的两个三角形相似。小结小结