垂直于弦的直径(2)VIP免费

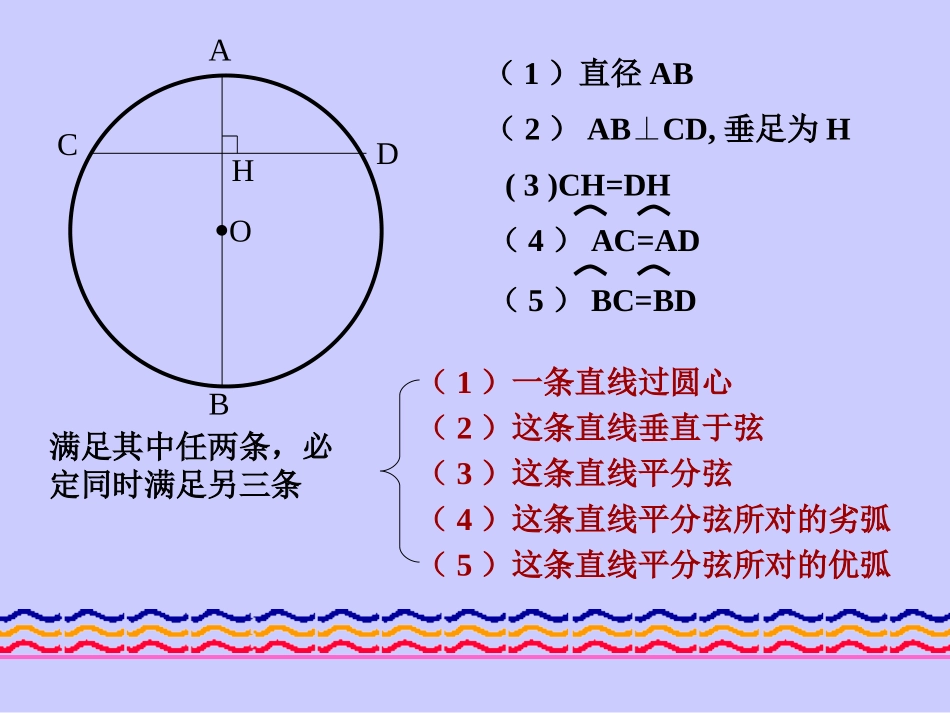
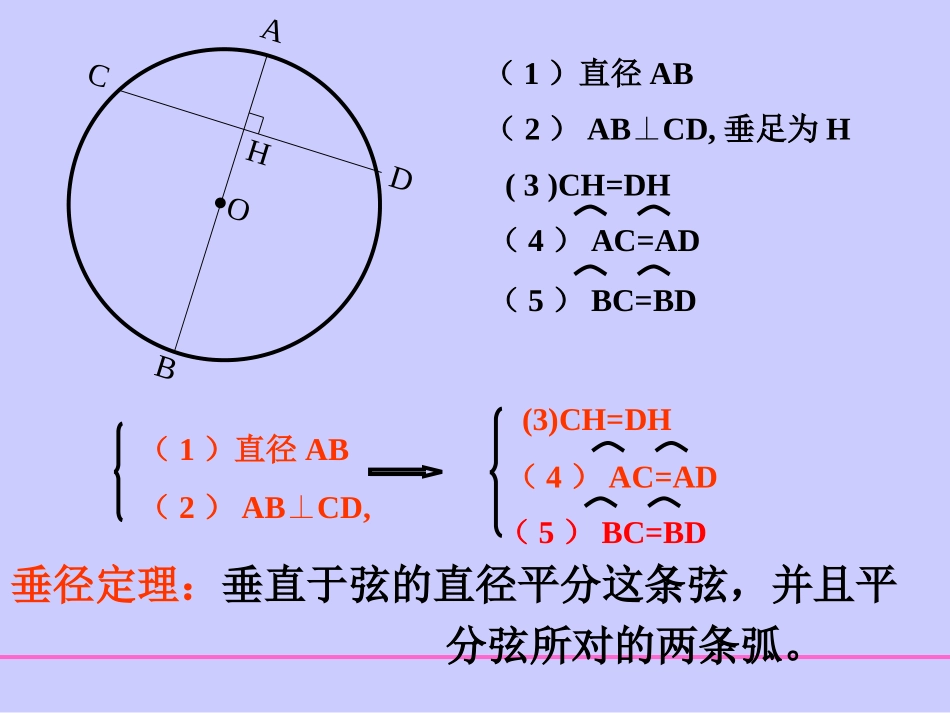
ABCDHO（1）直径AB（4）AC=AD(3)CH=DH满足其中任两条，必定同时满足另三条（1）一条直线过圆心（2）这条直线垂直于弦（3）这条直线平分弦（4）这条直线平分弦所对的劣弧（5）这条直线平分弦所对的优弧（5）BC=BD（2）ABCD,⊥垂足为H（1）直径AB（2）ABCD,⊥ABCDHO（1）直径AB（2）ABCD,⊥垂足为H（4）AC=AD(3)CH=DH（5）BC=BD（4）AC=AD(3)CH=DH（5）BC=BD垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的两条弧。（1）直径AB(3)CH=DHABCDHO（1）直径AB（2）ABCD,⊥垂足为H（4）AC=AD(3)CH=DH（5）BC=BD(2)ABCD⊥（4）AC=AD（5）BC=BD（1）平分弦（不是直径）的直径垂直于弦,并且平分这条弦所对的两条弧。推论1：ABCDHO(3)CH=DH(2)ABCD⊥（1）直径AB（4）AC=AD(3)CH=DH（5）BC=BD（1）直径AB（4）AC=AD（5）BC=BD（2）弦的垂直平分线经过圆心，并且平分弦所对的两条弧。推论1：（2）ABCD,⊥垂足为HABCDHO（1）直径AB（4）AC=AD（1）直径AB（2）ABCD,垂足为H（4）AC=AD(3)CH=DH（5）BC=BD(3)CH=DH(2)ABCD⊥（5）BC=BD（3）平分弦所对的一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧。推论1：垂径定理的推论1（1）平分弦（不是直径）的直径垂直于弦,并且平分这条弦所对的两条弧。（2）弦的垂直平分线经过圆心并且平分弦所对的两条弧。（3）平分弦所对的一条弧的直径，垂直平分弦，并且平分弦所对的另一条弧。垂径定理的推论2CDABHOMN圆的两条平行弦所夹的弧相等设AB是弦CD的垂直平分线，则AB是直径，且AC=AD①））设MN是平行于CD的另一条弦则MNAB⊥∴AM=AN②））由②—①得CM=DN））判断是非（1）平分弦的直径，平分这条弦所对的弧。（2）平分弦的直线，必定过圆心。（3）一条直线平分弦（这条弦不是直径），那么这条直线垂直这条弦。ABCDO(1)ABCDO(2)ABCDO(3)（4）弦的垂直平分线一定是圆的直径。（5）平分弧的直线，平分这条弧所对的弦。（6）弦垂直于直径，这条直径就被弦平分。ABCO(4)ABCDO(5)ABCDO(6)E按图填空ABMNOC①若MNAB,MN⊥为直径，则_______,__________,__________.AC=BCAN=BN))AM=BM))②若AC=BC,MN为直径则_________,__________,_________.ABMN⊥AN=BN))AM=BM))③若ABMN,AC=BC,⊥则______________,__________,________.MN为直径AN=BN))AM=BM))④若，MN为直径，则____________,___________,_________.AM=BM))AC=BCABMN⊥AN=BN))解：（1）AC=CB，OC是半径（已知）OCABADO=90OAB+AOC=90OAB=90-35=55ABCDO例1如图，在扇形OAB中，C是AB的中点，OC交AB于点DAOC=35,AD=16cm求：（1）OAB的度数（2）AB的长(平分弦所对的一条弧的直径，垂直于弦)(平分弦所对的一条弧的直径，平分这条弦)解：（2）AC=CB，CD经过圆心O（已知）DB=AD=16cmAB=2AD=32cmABCDOAB1.连接AB·ＣMND作法：例2平分已知AB.）已知：AB.求作：AB的中点.））2.作AB的垂直平分线CD，交AB于点D）点D就是所求AB的中点）小结1.主要通过对圆中四个条件的两两组合，得出了除了垂径定理以外的圆的另五条性质。2.注意这六条性质必须同时满足两个条件才能运用。（1）一条直线过圆心（2）这条直线垂直于弦（3）这条直线平分弦（4）这条直线平分弦所对的劣弧（5）这条直线平分弦所对的优弧推论2圆的两条平行弦所夹的弧相等推论1ACBDHO思考题：如图,圆O中，AB,CD是两条弦，E、F分别是AB，CD的中点，EF过圆心O，CDAB,为什么？E分析：CDABCFE=90BEF=90OFCDOEABOF过圆心OE过圆心点F是CD中点点E是AB中点ABCD.OFE