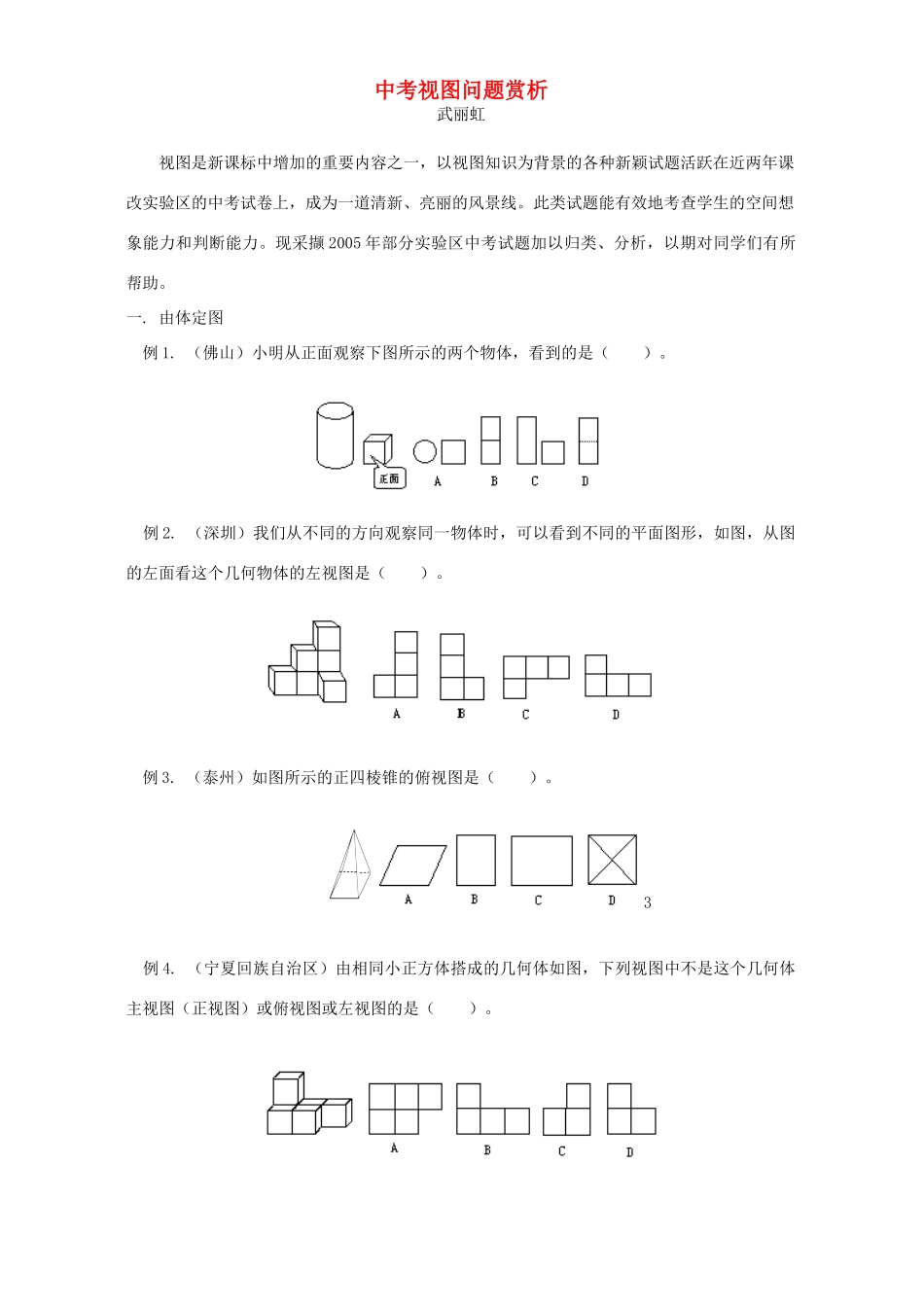
中考视图问题赏析武丽虹视图是新课标中增加的重要内容之一,以视图知识为背景的各种新颖试题活跃在近两年课改实验区的中考试卷上,成为一道清新、亮丽的风景线。此类试题能有效地考查学生的空间想象能力和判断能力。现采撷2005年部分实验区中考试题加以归类、分析,以期对同学们有所帮助。一.由体定图例1.(佛山)小明从正面观察下图所示的两个物体,看到的是()。例2.(深圳)我们从不同的方向观察同一物体时,可以看到不同的平面图形,如图,从图的左面看这个几何物体的左视图是()。例3.(泰州)如图所示的正四棱锥的俯视图是()。3例4.(宁夏回族自治区)由相同小正方体搭成的几何体如图,下列视图中不是这个几何体主视图(正视图)或俯视图或左视图的是()。评析:《数学课程标准》要求:会画简单几何体(直棱柱、圆柱、圆锥、球)的三视图(主视图、左视图、俯视图),会判断简单物体的三视图,即要求学生在给出简单的几何体条件下,画出正确的三视图,从而感受和体验空间与平面图形的现实意义,并初步体验二维与三维空间的相互转化的关系。例1从正面看;例2从左面看;例3从上面看;例4要从三个方向看,不难得到其答案应该分别选C、B、D、C。二.由图定体例5.(南京)下面四个几何体中,主视图、左视图与俯视图是全等图形的几何体是()。A.球B.圆柱C.三棱柱D.圆锥例6.(常州市)如果某物体的三视图是如图所示的三个图形,那么该物体的形状是()。A.正方体B.长方体C.三棱柱D.圆锥例7.(厦门)一个物体的正视图、俯视图如图所示,请你画出该物体的左视图并说出该物体形状的名称。评析:《数学课程标准》要求:能根据三视图来描述基本几何体或实物原型,也就是要求学生切实把握平面图形与实物的转化关系,从而培养逆向思维能力以及空间观念。以上三例能准确把握新课标的要求和精神,着眼基础。例5选择A;例6选择C;例7中左视图是个长方形(如图),该物体是个圆柱体。三.由图定图例8.(枣庄课改)一个几何体由一些小正方体组成,其主(正)视图与左视图如图所示。其俯视图不可能是()。例9.(沈阳)如图是由几个小立方块所搭几何体的俯视图,小正方形中的数字表示在该位置的小立方块的个数,这个几何体的主视图是()。评析:这两例考查了学生对“视图—几何体—视图”之间的相互关系的理解以及转化的能力;这是一个观察、想象、探索和分析的综合过程,体现了对“平面一空间一平面”的相互关系的理解、转化与把握。此类问题有一定的难度,对照所提供的视图,例8选C,例9选D。四.由图定数例10.(内江)桌上摆着一个由若干个相同正方体组成的几何体,其主视图和左视图如图所示,这个几何体最多可以由________个这样的正方体组成。例11.(聊城市)由若干个小立方体搭建的几何体的主视图和俯视图如图所示,则搭建这样的几何体至少用多少个小立方体()。A.5个B.6个C.7个D.8个评析:此类题型设计新颖,具有一定的探索性、综合性和挑战性。学生要依据图形的特征和视图的基本知识,寻求它们间的基本关系,探求符合要求的几何结构,从而确定立方体的个数。这类问题紧扣新课标,符合新课改精神,考查了学生读图、识图、获取信息的基本能力和观察、分析解决问题的能力。一般来讲,符合此类问题的正方体个数不惟一,例10中最多有13个,例11中至少有7个,选C。总之,弄清视图问题,要从现实生活中积累丰富的几何知识经验出发,在感知中构建空间观念,从而体验空间与图形的现实意义,有利于帮助学生提高自己的空间思维能力。相关练习:1.(河北课改)下图中几何体的主视图是()。2.(长沙市)下图中几何体的俯视图是()。3.(南通海门)“圆柱与球的组合体”如下图所示,则它的三视图是()。4.(遂宁课改)下列两个图是由几个相同的小长方体堆成的物体视图,那么堆成这个物体的小长方体最多有()个。A.5B.6C.4D.35.(山西课改)下图是由一些相同的小正方体构成的几何体的三视图。在这个几何体中,小正方体的个数是()。A.7B.6C.5D.4[参考答案]1.C2.B3.A4.A5.C