余弦函数的图像与性质VIP免费

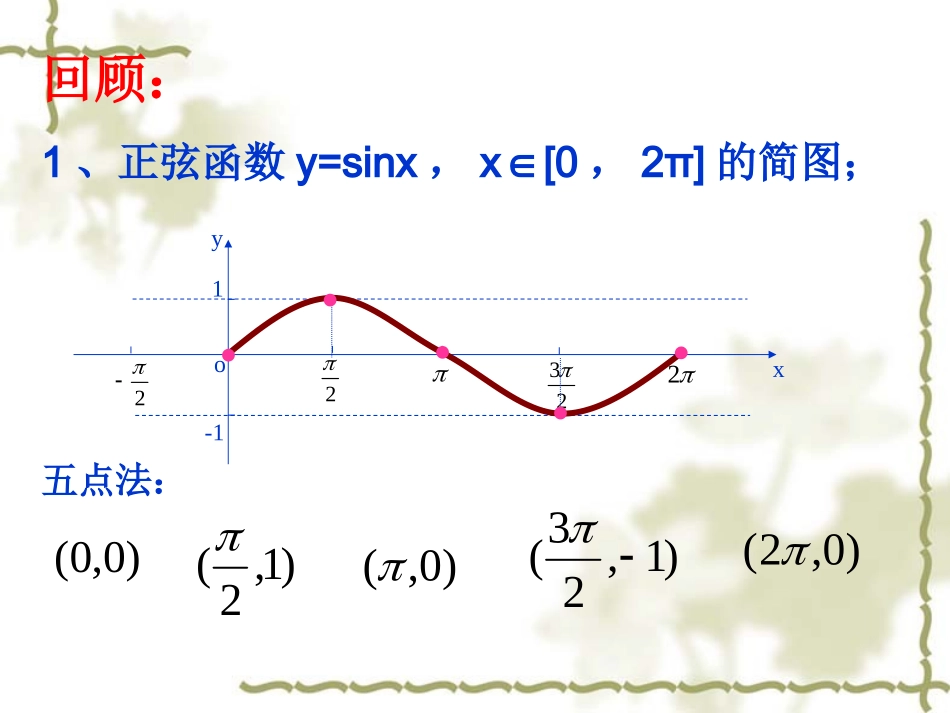
回顾：1、正弦函数y=sinx，x[0∈，2π]的简图；yxo1-122322五点法：)0,0()0,2()1,23()0,()1,2(x6yo--12345-2-3-41正弦曲线回顾思考：如何根据正弦函数的图像解：1(1)sin2x1(2)sin2x656函数y=sinx,图形定义域值域最值周期奇偶性单调性对称性2522320xy21-1R[1,1]y2对称轴：,2xkkZ对称中心：(,0)kkZ奇函数max2()12xkkZymin2()12xkkZy2,2()22kkkZ增区间32,2()22kkkZ减区间Rx:化简(使用诱导公式）sin(x)2cosx如何作余弦函数y=cosx(x∈R)的图象？cosyx只需将sinyx的图象向左平移2个单位即可得到。余弦曲线x02323y11sinyx232正弦曲线形状一样位置不同◎平移法：正弦、余弦函数的图象yxo1-122322y=cosx，x[0,2]y=sinx，x[0,2]xsinxcosx0002012-132横坐标相同纵坐标不同10-110◎五点作图法函数y=cosx，x[0,2]的简图xcosx2230210-101y=cosx，x[0,2]列表描点作图yxo1-122322x6yo--12345-2-3-41y=cosxx[0,2]y=cosxxRcos(x+2k)=cosx,kZ五点法：余弦函数y=cosx,xR∈的图象函数y=cosx,x∈R有哪些性质？x02323y11cosyx232232yxo--1234-2-31223252722325余弦函数的定义域，值域？y=1y=-1余弦函数的定义域:余弦函数的值域：R[-1，1]yxo--1234-2-31223252722325余弦函数的最值？2()xkkZ当时，函数值y取最大值12()xkkZ当时，函数值y取最小值-1yxo--1234-2-31223252722325余弦函数的周期？最小正周期：2cos(2)cosxkxkZ)0(2kZkk，也是它的周期余弦函数的奇偶性cos(-x)=cosx(xR)y=cosx(xR)是偶函数yxo--1234-2-31223252722325图象关于y轴对称余弦函数的单调性y=cosx(xR)增区间为其值从-1到1yxo--1234-2-31223252722325减区间为其值从1到-1Zkkk2,2[-,0]34，，2，，单调递增[-2,-]023，，，，单调递减Zkkk2,2yxo--1234-2-31223252722325余弦函数的对称性？对称轴：,2kZ（k+,0）,xkkZ对称中心：函数y=sinxy=cosx图形定义域值域最值周期奇偶性单调性对称性2522320xy21-1R[1,1]y2对称轴：,2xkkZ对称中心：(,0)kkZ奇函数max2()12xkkZymin2()12xkkZy2,2()22kkkZ增区间32,2()22kkkZ减区间2522320xy1-1R[1,1]y2max2()1xkkZy偶函数对称轴：,xkkZ对称中心：(,0)2kkZZkkk2,2增区间Zkkk2,2减区间RxRx1)(2minyZkkx典例1：求下列函数的最大值和最小值以及取得最大，最小值时x的值1cos3)1(xy（分析）利用余弦函数值域求cos12,3112xxkkZy当时，取最小值:（）cos1,2()(3)(1)14xxkkZy当即取最大值求函数的最大最小值？以及取得最大最小值时x的值课堂练习1：（1）y=2cosx-3解：（1）y=2cosx-3，当cosx=1时，y取得最大值：-1，此时：x=2()kkZ当cosx=-1时，y取得最小值：-5，此时：x=2()kkZ求函数的最大最小值？以及取得最大最小值时x的值课堂练习1：cos,1,1txt令)(2Zkkx也就是)(2Zkkx也就是1)23(cos)2(2xy1,1,1)23(2ttyy有最大值429y有最小值45,1cos,1xt即,1cos,1xt即典例2：判断下列函数的奇偶性：2cos)1(xy分析：利用函数的奇偶性定义判断cos2()cos2yxfxx把函...