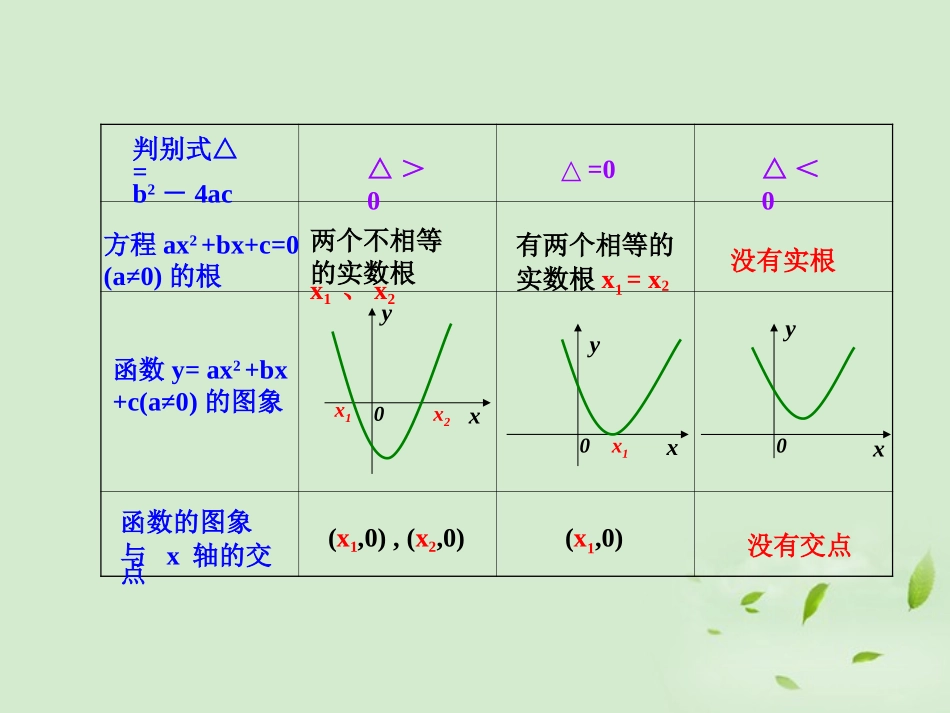
2.4.1函数的零点思考:一元二次方程ax2+bx+c=0(a≠0)的根与二次函数y=ax2+bx+c(a≠0)的图象有什么关系?方程ax2+bx+c=0(a≠0)的根函数y=ax2+bx+c(a≠0)的图象判别式△=b2-4ac△>0△=0△<0函数的图象与x轴的交点有两个相等的实数根x1=x2没有实根xyx1x20xy0x1xy0(x1,0),(x2,0)(x1,0)没有交点两个不相等的实数根x1、x2一般地,如果函数y=f(x)在实数处的值等于0,即f()=0,则叫做函数y=f(x)的零点。在坐标系中表示图像与x轴的公共点是(,0)点.方程f(x)=0有实数根函数y=f(x)的图象与x轴有交点函数y=f(x)有零点函数零点的定义:函数零点的定义:等价关系等价关系222bbb2222222对于二次函数y=ax+bx+c(a0):当+4ac>0时,方程ax+bx+c=0有两个不相等的实数根,这时说二次函数y=ax+bx+c有两个零点;当+4ac=0时,方程ax+bx+c=0有两个相等的实数根(重根)这时说二次函数y=ax+bx+c有一个二重零点或有二阶零点;当+4ac<0时,方程ax+bx+c=0没有实数根,这时二次函数y=ax+bx+c没有零点.方程的根与函数的零点之间的关系一.从二次函数的图像看函数零点的性质•当函数的图象通过零点且穿过X轴时,函数值变号.•两个零点把X轴分为三个区间:在每个区间上函数值保持同号.二求出二次函数的零点及其顶点坐标,又能粗略地画出函数草图,确定二次函数的一些主要性质.xyx1x201122(,),(,)(,)xxxx观察二次函数f(x)=x2-2x-3的图象:在区间[2,4]上,f(2)___0,f(4)___0,f(2)·f(4)___0在区间(2,4)上,x=3是x2-2x-3=0的另一个根.....xy0-132112-1-2-3-4-24零点存在性的探索><<<<>在区间[-2,1]上,f(-2)__0,f(1)___0,则f(-2)·f(1)___0,在区间(-2,1)上,x=-1是x2-2x-3=0的一个根如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a)·f(b)<0,那么,函数y=f(x)在区间(a,b)内有零点,即存在c(a,b)∈,使得f(c)=0,这个c也就是方程f(x)=0的根。注注::只要满足上述两个条件只要满足上述两个条件,,就能判断函数在就能判断函数在指定区间内存在零点。指定区间内存在零点。结论:xy01......ab....xy0..ab1、对于定义在R上的函数y=f(x),若f(a).f(b)<0(a,bR,且a–2Bx<–2Cx>2Dx<23、函数f(x)=x3-16x的零点为()A(0,0),(4,0)B0,4C(–4,0),(0,0),(4,0)D–4,0,44、函数f(x)=–x3–3x+5的零点所在的大致区间为()A(1,2)B(–2,0)C(0,1)D(0,)21BBDA5、已知函数f(x)的图象是连续不断的,有如下的x,f(x)对应值表:x1234567f(x)239–711–5–12–26那么函数在区间[1,6]上的零点至少有()个A5B4C3D2C确定函数零点所在大致区间及零点个数的方法、步骤:(1)作出x、f(x)的对应值表格;(2)作出y=f(x)的图象;(3)确定y=f(x)的单调性情况(4)作出判断。归纳、小结小结与思考函数零点的定义等价关系等价关系函数的零点或相应方程的根的存在性以及个数的判断作业成才之路:2.4.1函数零点P91--P92