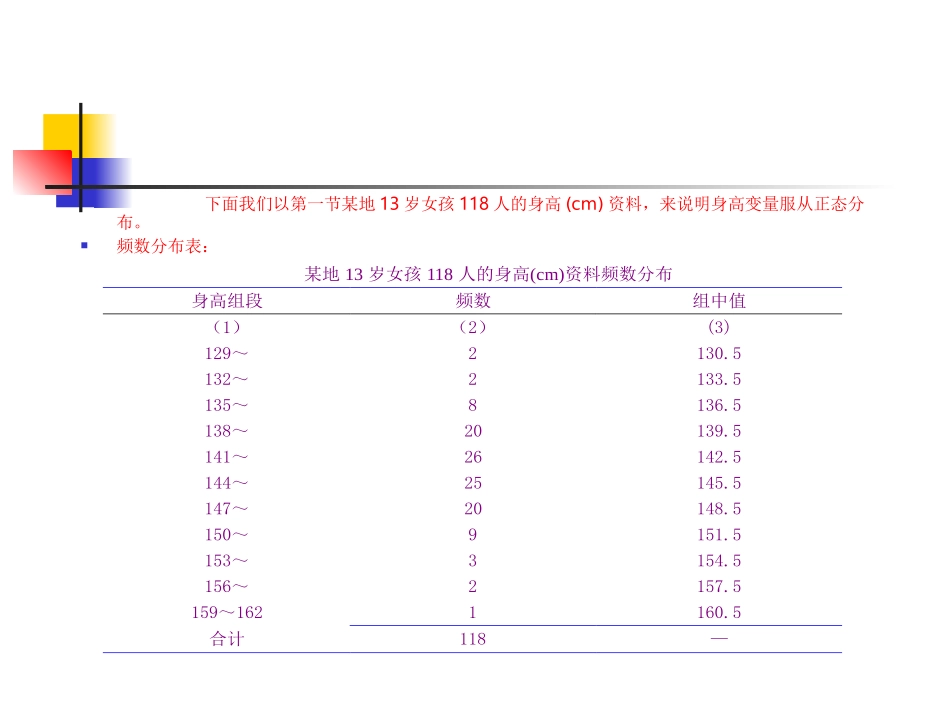
正态分布正态分布的通俗概念:如果把数值变量资料编制频数表后绘制频数分布图(又称直方图,它用矩形面积表示数值变量资料的频数分布,每条直条的宽表示组距,直条的面积表示频数(或频率)大小,直条与直条之间不留空隙。),若频数分布呈现中间为最多,左右两侧基本对称,越靠近中间频数越多,离中间越远,频数越少,形成一个中间频数多,两侧频数逐渐减少且基本对称的分布,那我们一般认为该数值变量服从或近似服从数学上的正态分布。正态分布的概念下面我们以第一节某地13岁女孩118人的身高(cm)资料,来说明身高变量服从正态分布。频数分布表:某地13岁女孩118人的身高(cm)资料频数分布身高组段频数组中值(1)(2)(3)129~2130.5132~2133.5135~8136.5138~20139.5141~26142.5144~25145.5147~20148.5150~9151.5153~3154.5156~2157.5159~1621160.5合计118—频数分布图一(又称直方图)(cm)身高160.5157.5154.5151.5148.5145.5142.5139.5136.5133.5130.513118(cm)某地岁女孩人身高频数分布图频数3020100从频数表及频数分布图上可得知:该数值变量资料频数分布呈现中间频数多,左右两侧基本对称的分布。所以我们通俗地认为该资料服从正态分布。(cm)身高13118(cm)某地岁女孩人身高频数分布图频数20100频数分布图二频数分布图三(cm)身高13118(cm)某地岁女孩人身高频数分布图频数14121086420正态分布图四(cm)身高频数分布逐渐接近正态分布示意图正态分布的数理统计学概念:如果随机变量(X)的概率密度函数为:-∞<x<+∞则该随机变量服从正态分布。式中σ为总体标准差;μ为总体均数;π为圆周率,即3.14159···;e为自然对数的底,即2.71828···。22221xexf若某一随机变量的概率密度函数(频率曲线方程)为上式,则称该变量X服从参数为μ和σ的正态分布,记为:X~N(μ,σ2)。函数方程中μ为位置参数,σ为形状参数。在σ不变的情况下,函数曲线形状不变,若μ变大时,曲线位置向右移;若μ变小时,曲线位置向左移。在μ不变的情况下,函数曲线位置不变,若σ变大时,曲线形状变的越来越“胖”和“矮”;若σ变小时,曲线形状变的越来越“瘦”和“高”。若某一随机变量X,其总体均数μ=0,总体标准差σ=1,即X~N(0,1),则称变量X服从标准正态分布。习惯把服从标准正态分布的变量用字母U或Z表示,此时,我们把U或Z称为标准正态变量。标准正态分布是正态分布中的一个典型分布,数理统计上证明:对一服从正态分布的随机变量(X),若进行特定的变量变换,可将任何一服从正态分布的随机变量(X)转变成服从标准正态分布的随机变量(U或Z),这种变量变换过程称为变量的标准化,也称为U或Z变换。式中符号意义如前述。XU正态分布的特征及其面积规律正态分布曲线位于横轴上方,呈钟形。正态分布曲线以均数所在处最高,且以均数为中心左右对称。0f(x)maxµσ=0.50f(x)µσ=1σ=20f(x)maxµ1µ2正态分布曲线由两个参数决定,即总体均数μ和总体标准差σ。在σ不变的情况下,函数曲线形状不变,若μ变大时,曲线位置向右移;若变小时,曲线位置向左移,故称μ为位置参数。在μ不变的情况下,函数曲线位置不变,若σ变大时,曲线形状变的越来越“胖”和“矮”;若σ变小时,曲线形状变的越来越“瘦”和“高”,故称σ为形态参数或变异度参数。N(μ,0.52)、N(μ,12)、N(μ,22)N(μ1,σ2)、N(μ2,σ2)正态曲线下面积分布有一定的规律性。对于服从正态分布的随机变量(X),随机变量值出现在某一区间(x1,x2)的概率与正态分布概率密度曲线与横轴在该区间所围成的区域的面积大小相对应(相等)。正态分布概率密度曲线与横轴围成的区域的总面积恒等于1。正态分布概率密度曲线下横轴上一定区间的面积可应用数学知识求出。在实际应用中,由于所有正态分布都可以通过变量变换转变为标准正态分,为了省去积分计算不同正态分布曲线下横轴上一定区间面积的繁琐过程,所以数理统计学家专门编制了标准正态分布曲线下横轴上一定区间面积分布表,供查表求标准正态分布曲线下一定区间面积。标准正态分布...