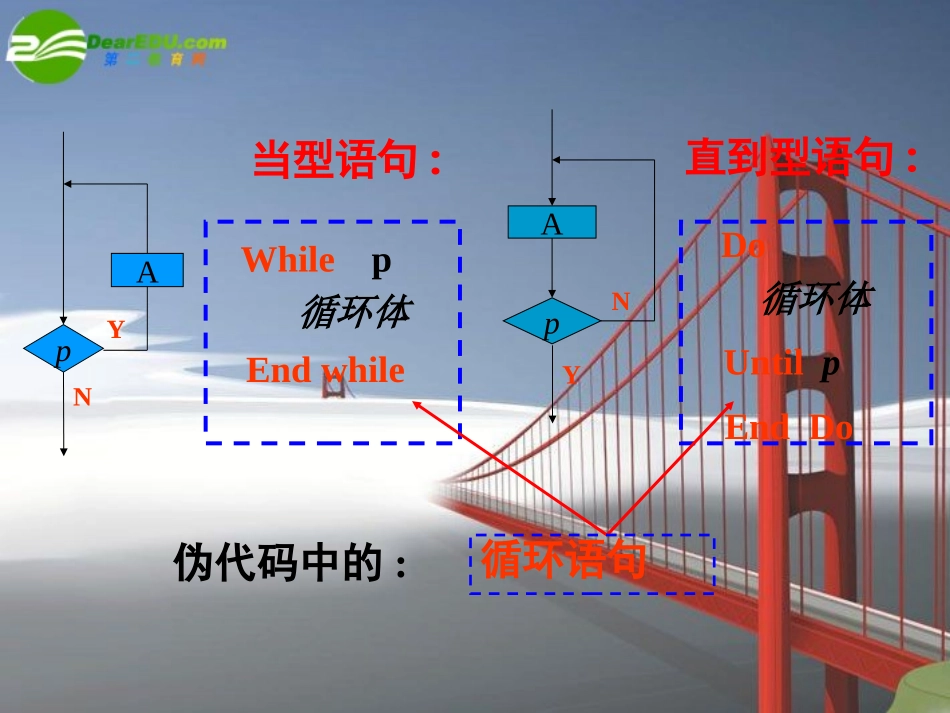
已学过的伪代码中的几种基本算法语句:(1)赋值语句:变量←表达式或变量或常数.(2)输入语句:Reada,b(3)输出语句:(4)条件语句:Printa,bIfAThenBElseCEndIf复习当型语句:Whilep循环体Endwhile直到型语句:Do循环体UntilpEndDo循环语句伪代码中的:pAYNpAYN当循环的次数已经确定,可用“For”语句表示.“For”语句伪代码格式:ForIFrom“初值”To“终值”step“步长”……EndFor35915在小学,我们学过求两个正整数的最大公约数的方法,先用两个数公有的质因数连续去除,一直到所得的商是互质数为止,然后把所以的除数乘起来,例如,求18与30的最大共约数:183023所以,18与30的最大共约数是:2×3=6.引入写出求两个正整数a,b(a>b)的最大公约数的一个算法案例2公元前3世纪,欧几里得在《原本》第七篇中介绍了求两个正整数a,b(a>b)的最大公约数的方法,即求出一列数:.0,,,,,,,121nnrrrrba这列数从第三项开始,每一项都是前两项相除所得的余数,余数为0的前一项rn,即是a和b的最大公约数。这种方法称为“欧几里得辗转相除法”辗转相除法•例1用辗转相除法求a=204和b=85的最大公约数。;3428520434,852041,所以为余数r•分析:;172348517,34852,所以为余数r.217340,17341,所以为余数r因此,204与85的最大公约数是r2=17.•欧几里得辗转相除法找出a,b的最大公约数的步骤是:•(1)计算a÷b的余数r,若r=0,则b为a,b的最大公约数;•(2)若r≠0,则把前面的除数b作为新的被除数,把余数r作为新的除数,继续运算,直到余数为0,此时的除数即为a,b的最大公约数.求a,b(a>b)的最大公约数的算法为:S1输入两个正整数a,b;S2如果Mod(a,b)≠0,那么转S3,否则转S6;S3r←Mod(a,b);S4a←b;S5b←r,转S2;S6输出b.r←MOD(a,b)a←bb←rr=0是否Reada,bWhileMod(a,b)≠0r←Mod(a,b)a←bb←rEndWhilePrintbEnd流程图与伪代码回顾反思辗转相除法是当大数被小数除尽时,结束除法运算,较小的数就是最大公约数.求三个以上(含三个数)的数的最大公约数时,可依次通过求两个数的最大公约数与第三数的最大公约数来求得.课外作业直通车相应练习