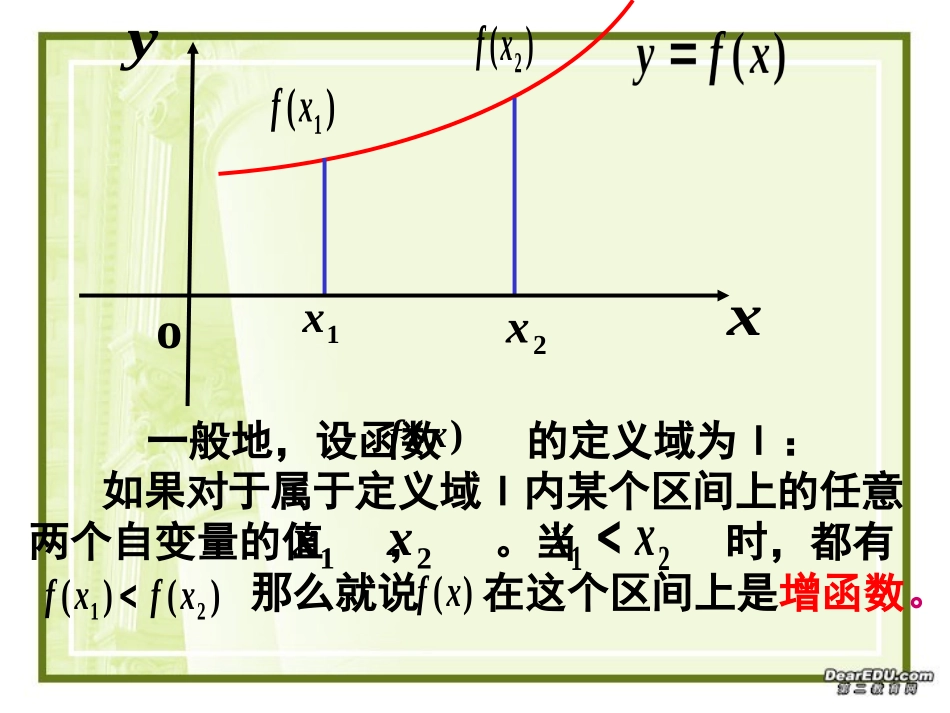
观察函数y=x2的图象观察函数y=x3的图象图象1图象2函数y=x2在对称轴x=0的左侧,函数值随着x的增大而减小;在对称轴x=0的右侧,函数值随着x的增大而增大用数学语言来表示:任意x1,x2(-∞,0]∈且x1f(x2).任意x1,x2[0,+∞,],∈且x10,则为减函数).(下结论)属于x,x2121xx)()(21xfxf例4证明函数在(0,+∞)上是减函数.xxf1)(证明:设是(0,+∞)上的任意两个实数,且,则21,xx21xx2112212111)()(xxxxxxxfxf由,得),0(,22xx021xx又由,得21xx012xx于是,即0)()(21xfxf)()(21xfxf所以,在(0,+∞)上是减函数.xxf1)(例4证明函数在(-∞,0)上是减函数.xxf1)(证明:设是(-∞,0)上的任意两个实数,且,则21,xx21xx2112212111)()(xxxxxxxfxf由,得)0,(x,x22021xx又由,得21xx012xx于是,即0)()(21xfxf)()(21xfxf所以,在(0,+∞)上是减函数.xxf1)()是减函数(0,,0)在(x1f(x)否说)也是减函数,那么能(0,间,0)是减函数,在区在区间(x1数f(x)思考:现在已经知道函.0[xf1aax1xxf52)上是单调函数,)在区间(证明)(其中常数)(:设函数例)上是单调减函数.0,函数f(x)在区间[)f(x)即f(x0a)1x1xxx)(x(x)f(x)f(x0a1axxxxa1x1xxx1且a,xx00xx,xxa)1x1xxx)(x(x)xa(x1x1xxx)f(x)f(xx)且x[0,x,x:证明212222121212222122221212121222212121222222121212111111小结:今天我们主要学习了函数的单调性.函数的单调性是函数的一个局部性质,因此在说一个函数的单调性时必须讲明是针对哪个区间.另外还好掌握证明一个给定函数在给定区间上的单调性的一般步骤:取值,作差