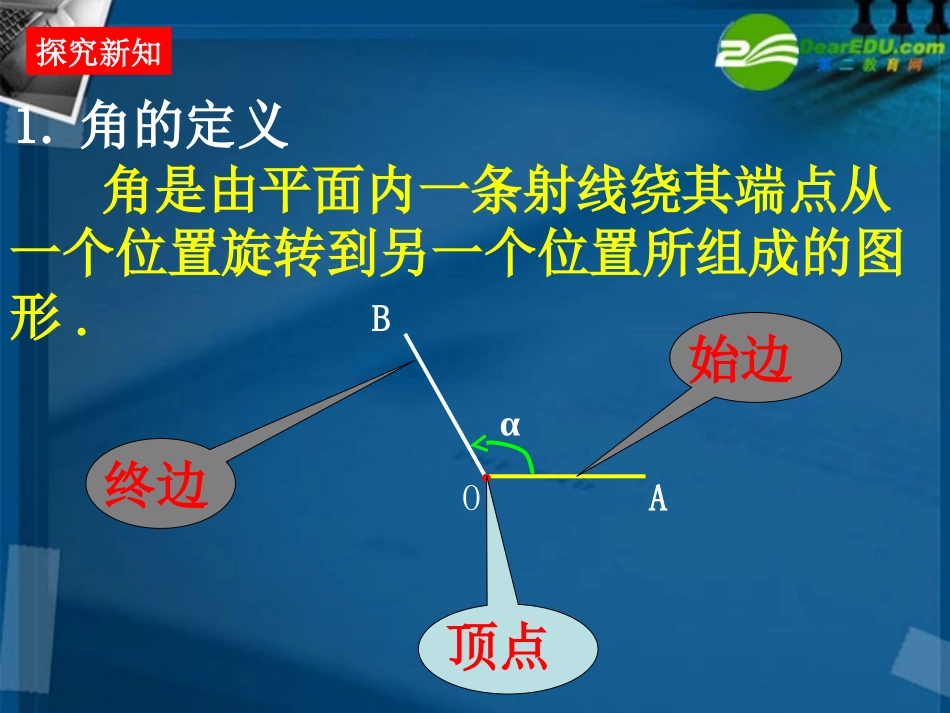
1.1任意角第一章三角函数高一年级数学必修42002年11月22日,在匈牙利德布勒森举行的第36届世界体操锦标赛中,“李小鹏跳”——“踺子后手翻转体180度接直体前空翻转体900度”,震惊四座,这里的转体180度、转体900度就是一个角的概念.探究新知探究新知1.角的定义角是由平面内一条射线绕其端点从一个位置旋转到另一个位置所组成的图形.AOBα始边终边顶点126312457891011300-300126312457891011900-1200规定:按逆时针方向旋转形成的角叫做正角,按顺时针方向旋转形成的角叫做负角.如果一条射线没有作任何旋转,则称它形成了一个零角.2.正角、负角、零角探究新知1263124578910114320xy03.象限角在直角坐标系中,角的顶点与原点重合,角的始边与x轴的非负半轴重合.xoy如果角的终边在第几象限,我们就说这个角是第几象限的角;如果角的终边在坐标轴上,就认为这个角不属于任何象限,或称这个角为轴线角.指出下列各角:-50°,405°,210°,-200°,-450°分别是第几象限的角?-50°xyoxyo210°-450°xyo405°xyo-200°xyo练习:思考1:锐角是第几象限的角?钝角?直角?思考3:第二象限的角一定比第一象限的角大吗?探究新知思考2:第一象限的角一定是锐角吗?象限角只能反映角的终边所在象限,不能反映角的大小.思考4:在直角坐标系中,135°角的终边在什么位置?xyo探究新知终边在该位置的角一定是135°吗?xyo思考5:与135°角终边相同的角有多少个?这些角与135°角在数量上相差多少?探究新知思考6:所有与135°角终边相同的角,连同135°角在内,可构成一个集合S,你能用描述法表示集合S吗?任一与α终边相同的角,都可以表示成角α与整数个周角的和.探究新知4.终边相同的角所有与角α终边相同的角,连同角α在内所构成的集合:S={β|β=α+k·360°,k∈Z}例1在0°~360°范围内,找出与-950°12′角终边相同的角,并判定它是第几象限角.129°48′,第二象限角.思考1:第一、二、三、四象限的角的集合分别如何表示?思考2:终边在x轴非负半轴、非正半轴,y轴非负半轴、非正半轴上的角分别如何表示?思考3:终边在x轴、y轴上的角的集合分别如何表示?S={α|α=45°+k·180°,k∈Z}.-315°,-135°,45°,225°,405°,585°.例2写出终边在直线y=x上的角的集合S,并把S中适合不等式-360°≤<720°的元素写出来.例3如果α是第二象限的角,那么α/2分别是第几象限的角?90°+k·360°<α<180°+k·360°45°+k·180°<α/2<90°+k·180°180°+k·720°<2α<360°+k·720°课后作业P9A组1、2、3