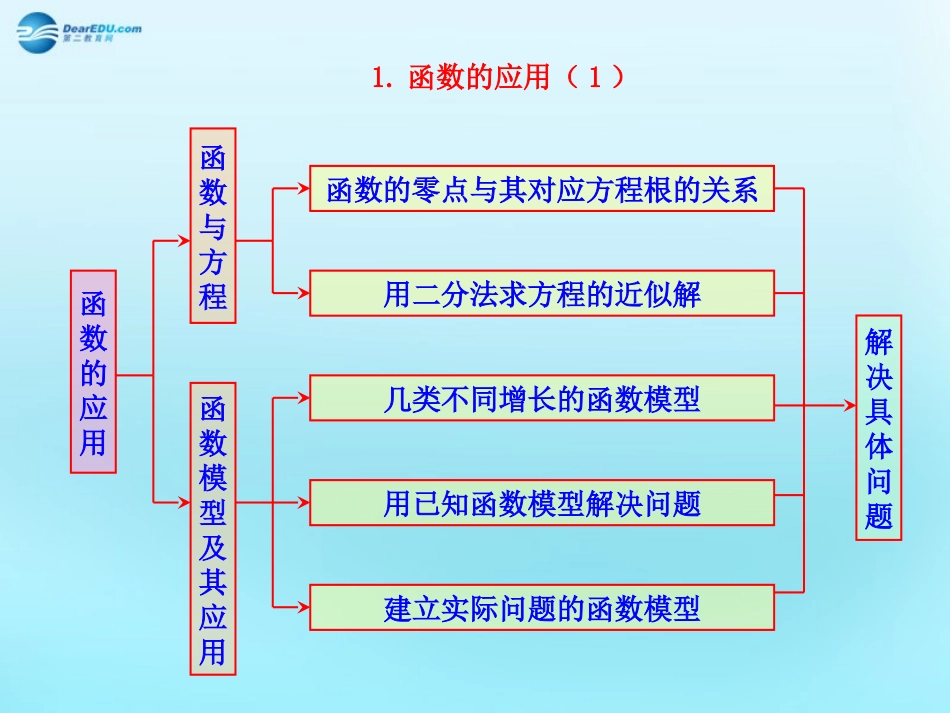
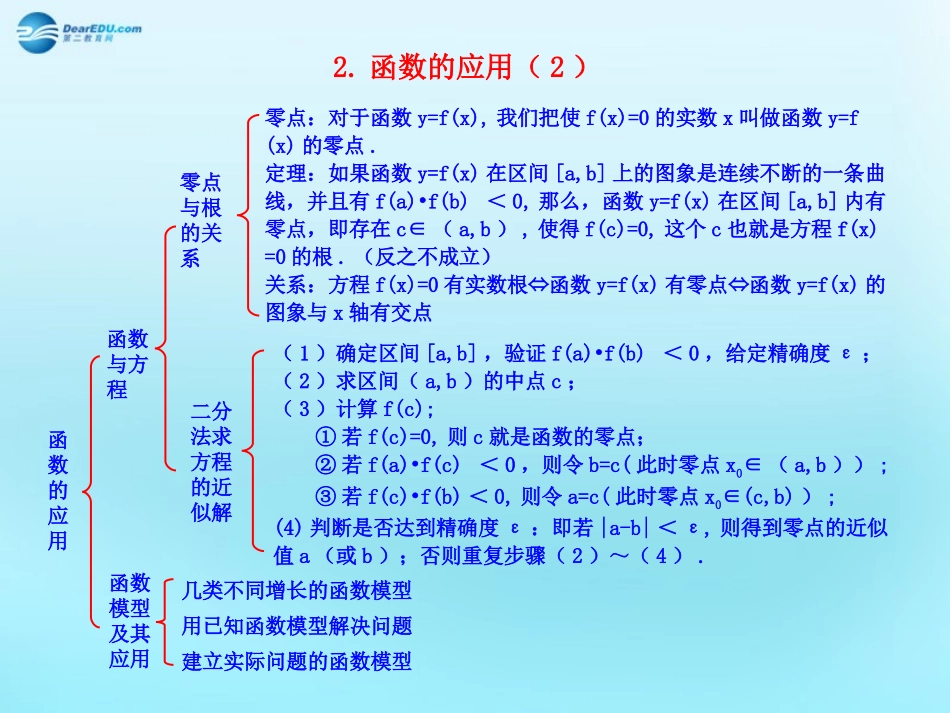
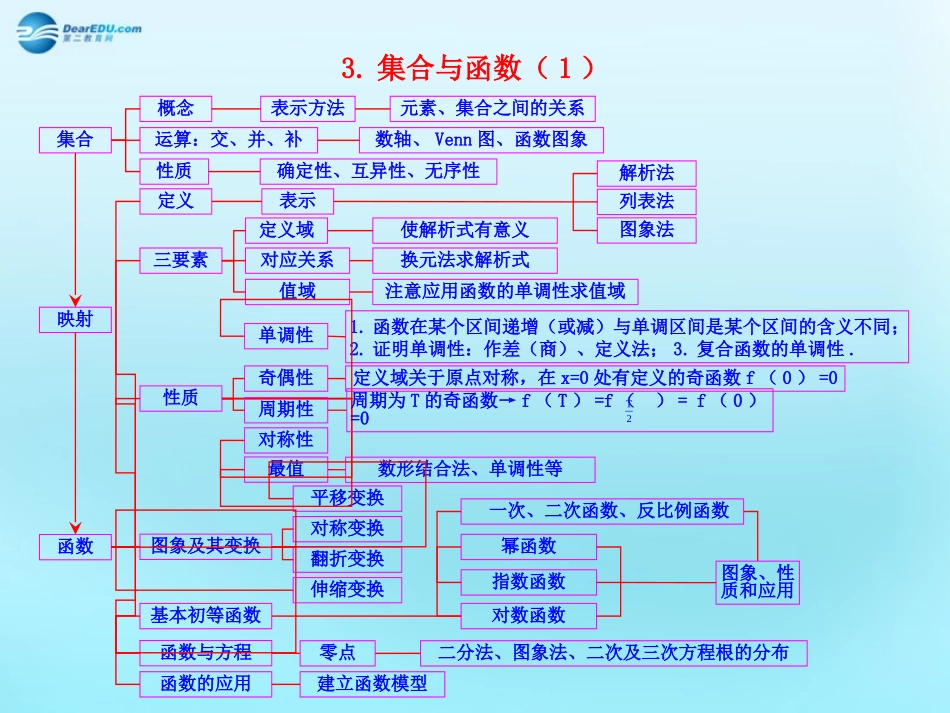
函数的应用函数与方程函数模型及其应用函数的零点与其对应方程根的关系用二分法求方程的近似解几类不同增长的函数模型用已知函数模型解决问题建立实际问题的函数模型解决具体问题1.函数的应用(1)2.函数的应用(2)函数的应用函数与方程零点与根的关系零点:对于函数y=f(x),我们把使f(x)=0的实数x叫做函数y=f(x)的零点.定理:如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a)•f(b)<0,那么,函数y=f(x)在区间[a,b]内有零点,即存在c∈(a,b),使得f(c)=0,这个c也就是方程f(x)=0的根.(反之不成立)关系:方程f(x)=0有实数根函数⇔y=f(x)有零点函数⇔y=f(x)的图象与x轴有交点二分法求方程的近似解(1)确定区间[a,b],验证f(a)•f(b)<0,给定精确度ε;(2)求区间(a,b)的中点c;(3)计算f(c);①若f(c)=0,则c就是函数的零点;②若f(a)•f(c)<0,则令b=c(此时零点x0∈(a,b));③若f(c)•f(b)<0,则令a=c(此时零点x0∈(c,b));(4)判断是否达到精确度ε:即若|a-b|<ε,则得到零点的近似值a(或b);否则重复步骤(2)~(4).函数模型及其应用几类不同增长的函数模型用已知函数模型解决问题建立实际问题的函数模型3.集合与函数(1)集合概念表示方法元素、集合之间的关系运算:交、并、补数轴、Venn图、函数图象性质确定性、互异性、无序性映射函数定义表示解析法列表法图象法三要素性质图象及其变换基本初等函数函数与方程函数的应用建立函数模型零点二分法、图象法、二次及三次方程根的分布定义域使解析式有意义对应关系换元法求解析式值域注意应用函数的单调性求值域单调性1.函数在某个区间递增(或减)与单调区间是某个区间的含义不同;2.证明单调性:作差(商)、定义法;3.复合函数的单调性.奇偶性定义域关于原点对称,在x=0处有定义的奇函数f(0)=0对称性最值数形结合法、单调性等平移变换对称变换翻折变换伸缩变换一次、二次函数、反比例函数幂函数指数函数对数函数图象、性质和应用周期性周期为T的奇函数→f(T)=f()=f(0)=0T2推广集合概念元素特性确定性互异性无序性表示方法列举法描述法图示法关系属于关系包含关系运算并集交集补集函数概念定义域对应关系值域表示方法基本性质列表法图象法解析法单调性与最大(小)值奇偶性概念映射研究定义特殊化4.集合与函数(2)