高二数学双曲线的标准方程课件 苏教版 课件VIP免费

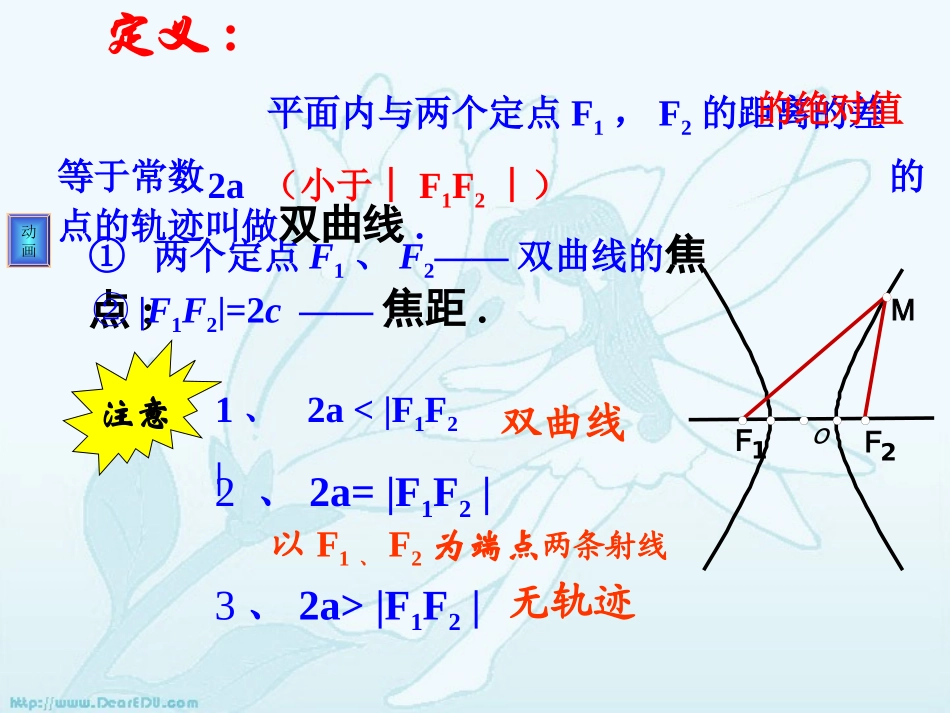
1.椭圆的定义动画和等于常数2a(2a>|F1F2|>0)的点的轨迹.平面内与两定点F1、F2的距离的1F2F0,c0,cXYOyxM,)0(12222babyax①两个定点F1、F2——双曲线的焦点;②|F1F2|=2c——焦距.oF2F1M平面内与两个定点F1，F2的距离的差等于常数的点的轨迹叫做双曲线.动画的绝对值2a（小于︱F1F2︱）注意定义:1、2a<|F1F2|双曲线2、2a=|F1F2|以F1、F2为端点两条射线3、2a>|F1F2|无轨迹xyo设P（x,y）,双曲线的焦距为2c（c>0）,F1(-c,0),F2(c,0)常数=2aF1F2P即|(x+c)2+y2-(x-c)2+y2|=2a以F1,F2所在的直线为X轴，线段F1F2的中点为原点建立直角坐标系1.建系.2.设点．3.列式．|PF1-PF2|=2a4.代点化简.移项两边平方后整理得：222cxaaxcy两边再平方后整理得：22222222caxayaca由双曲线定义知：22caca220ca设2220cabb代入上式整理得：222210,0xyabab即：12222byax12222bxayF2F1PxOyOPF2F1xy222(0,0)ababc双曲线的标准方程问题：如何判断双曲线的焦点在哪个轴上？问题：如何判断双曲线的焦点在哪个轴上？定义图象方程焦点a.b.c的关系1212202MFMFaaFF，22221xyab22221yxab,0Fc0,Fc222cab[练习]写出双曲线的标准方程1、已知a=3,b=4焦点在x轴上，双曲线的标准方程为。2、已知a=3,b=4焦点在y轴上，双曲线的标准方程为。116922yx116922xy[练习]判断下列各双曲线方程焦点所在的坐标轴；求a、b、c各为多少？11625)1(22yx3694)3(22yx3694)4(22yx14922yx11625)2(22xy194)4(22xy例1已知双曲线的焦点为F1(-5,0),F2(5,0)，双曲线上一点P到F1、F2的距离的差的绝对值等于8，求双曲线的标准方程.∵∵22aa=8,=8,c=5c=5∴∴aa=4,c=5=4,c=5∴∴bb22=5=522--4422=9=9所以所求双曲线的标准方程为：所以所求双曲线的标准方程为：191622yx根据双曲线的焦点在根据双曲线的焦点在xx轴上，设它的标准方程轴上，设它的标准方程为：为：)0,0(12222babyax解:例2求适合下列条件的双曲线的标准方程:a=52，经过点A（2，-5），焦点在y轴上。因为焦点在y轴上，所以双曲线方程可设为12222bxay因为a=52且点A（2,5)在双曲线上，所以14255222baa解得：2b＝16所以，所求双曲线的方程为：1162022xy练习1:如果方程表示双曲线，求m的取值范围.11mym2x22分析:方程表示双曲线时，方程表示双曲线时，则则mm的取值的取值范围是范围是_________________._________________.11mym2x22变式:2m1得0)1m)(m2(由2m1m或练习2:证明椭圆与双曲线19y25x22x2-15y2=15的焦点相同.定义方程焦点a.b.c的关系x2a2-y2b2=1x2y2a2+b2=1F（±c，0）F（±c，0）a>0，b>0，但a不一定大于b，c2=a2+b2a>b>0，a2=b2+c2双曲线与椭圆之间的区别与联系：双曲线与椭圆之间的区别与联系：||MF1|－|MF2||=2a|MF1|+|MF2|=2ax2a2+y2b2=1椭圆双曲线y2x2a2-b2=1F（0，±c）F（0，±c）小结•本节课学习了双曲线的标准方程并会根据已知条件来求出双曲线的标准方程.•大家注意双曲线与椭圆的异同点.特别是焦点的判断和a,b,c之间的关系.