高二数学双曲线的标准方程课件示例一 课件VIP免费

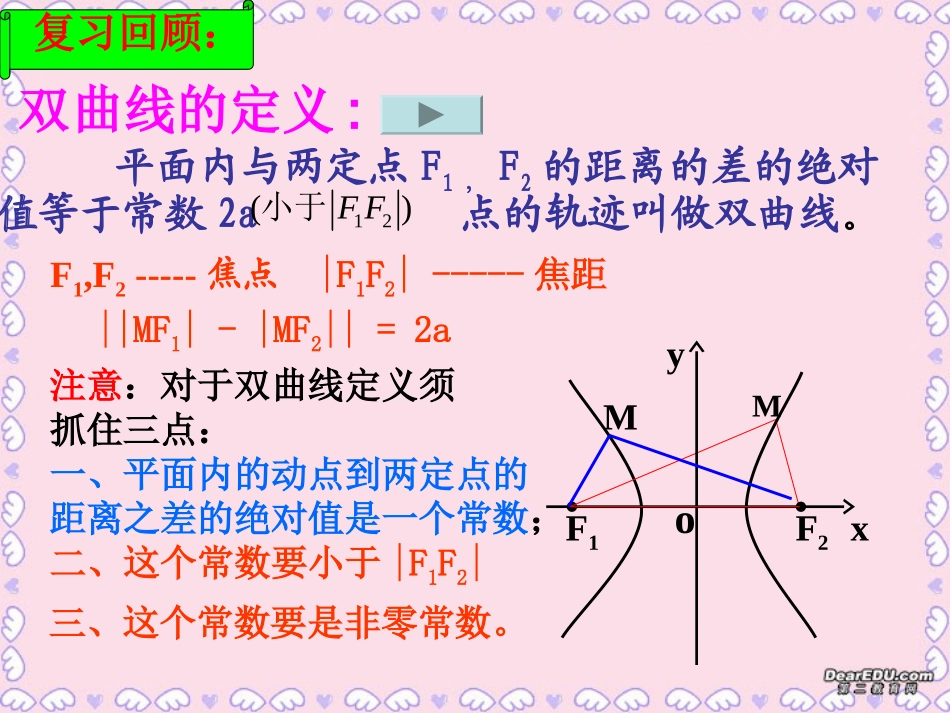
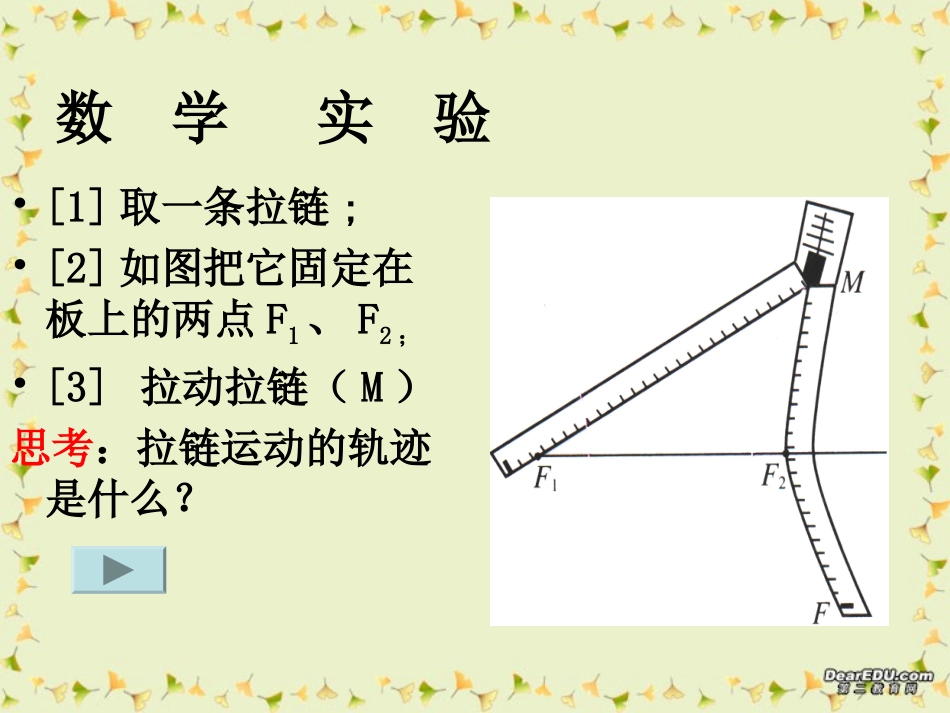
双曲线的定义:平面内与两定点F1，F2的距离的差的绝对值等于常数2a点的轨迹叫做双曲线。12()FF小于F1,F2-----焦点||MF1|-|MF2||=2a|F1F2|-----焦距.F2.F1Myox注意：对于双曲线定义须抓住三点：一、平面内的动点到两定点的距离之差的绝对值是一个常数；二、这个常数要小于|F1F2|M复习回顾：三、这个常数要是非零常数。数学实验•[1]取一条拉链;•[2]如图把它固定在板上的两点F1、F2；•[3]拉动拉链（M）思考：拉链运动的轨迹是什么？请思考？1、平面内与两定点的距离的差等于常数2a（小于|F1F2|）的轨迹是什么？2、平面内与两定点的距离的差的绝对值等于常数（等于|F1F2|）的轨迹是什么？3、平面内与两定点的距离的差的绝对值等于常数（大于|F1F2|）的轨迹是什么？双曲线的一支是在直线F1F2上且以F1、F2为端点向外的两条射线不存在相关结论：1、当||MF1|-|MF2||=2a<|F1F2|时，2、当||MF1|-|MF2||=2a=|F1F2|时，3、当||MF1|-|MF2||=2a>|F1F2|时,M点的轨迹不存在4、当||MF1|-|MF2||=2a=0时，M点轨迹是双曲线其中当|MF1|-|MF2|=2a时，M点轨迹是与F2对应的双曲线的一支；当|MF2|-|MF1|=2a时，M点轨迹是与F1对应的双曲线的一支.M点轨迹是在直线F1F2上且以F1和F2为端点向外的两条射线。M点的轨迹是线段F1F2的垂直平分线。设双曲线的焦距为,双曲线上任意一点到焦点的距离的差的绝对值等于常数2cp12,FF2a0)ca（P1F2Fxy0以所在的直线为轴,线段的垂直平分线为轴,建立直角坐标系12,FFx12,FFy则的坐标分别是12,FF,(-c,0)(c,0)12(,),||2PxyPFPFa设则2222|))|2xcyxcya即：（（化简：222220,0(0)cacabcab故令：22221(0,0)xyabab方程可化为：x表示焦点在轴上的双曲线。二、双曲线的标准方程：22222222caxayaca（）（）思考：我们还可以怎么建立坐标系？P2F1Fxy01212FFyFFx以所在的直线为轴，以线段的垂直平分线为轴建立坐标系12FF则，的坐标分别是(0,-c),(0,c)12(,),||2PxyPFPFa设则2222|)|2xycxyca即：（）（2222|))|2xcyxcya（（,xy对比两个方程可发现，仅互换了22221(0,0)yxababy表示焦点在轴上的双曲线。定义图象方程焦点a.b.c的关系1212202MFMFaaFF，22221xyab22221yxab,0Fc0,Fc222cab谁正谁对应a定义方程焦点a.b.c的关系x2a2-y2b2=1x2y2a2+b2=1F（±c，0）F（±c，0）a>0，b>0，a,b大小不确定，c2=a2+b2a>b>0，a2=b2+c2双曲线与椭圆之间的区别与联系：双曲线与椭圆之间的区别与联系：||MF1|－|MF2||=2a|MF1|+|MF2|=2ax2a2+y2b2=1椭圆双曲线y2x2a2-b2=1F（0，±c）F（0，±c）222222116921643634936xyxyxy练习1：根据双曲线的方程指出焦点坐标：（1）（）（）12(5,0)(5,0)FF12(0,10)(0,10)FF12(13,0)(13,0)FF例1已知双曲线的焦点为F1(-5,0),F2(5,0)，双曲线上一点P到F1、F2的距离的差的绝对值等于8，求双曲线的标准方程. 22aa=8,=8,c=5c=5∴∴aa=4,c=5=4,c=5∴∴bb22=5=522--4422=9=9所以所求双曲线的标准方程为：所以所求双曲线的标准方程为：191622yx根据双曲线的焦点在根据双曲线的焦点在xx轴上，设它的标准方程轴上，设它的标准方程为：为：)0,0(12222babyax解:221916xy221169xy221927yx轴上；焦点在经过点）（轴上；焦点在曲线的标准方程：：求适合下列条件的双例yAaxba),5,2(,522,4,3)1(2,4,3)1(轴上且焦点在由题意解：xba所以双曲线的方程为：116922yx.)2(轴上焦点在y12222bxay可设所求双曲线方程为由题意得：14255222baa162b解得1162022xy所求双曲线方程为练习3：（1）已知双曲线的焦点在y轴上，并且双曲线上两点P1、P2的坐标分别为（3，）、（9/4,5），求双曲线的标准方程.24解：因为双曲线的焦点在y轴上，所以设所求双曲线的标准方程为：12222bxay把点P1、P2的坐标代入双曲线方程得：1)49(2513)24(2222222baba解得：a2=16,b2=9.故所求双曲线的标准方程为：.191622xy例3:如果方程表示双曲线，求m的取值范围....