高考数学 基本初等函数(Ⅱ)总复习课件VIP免费

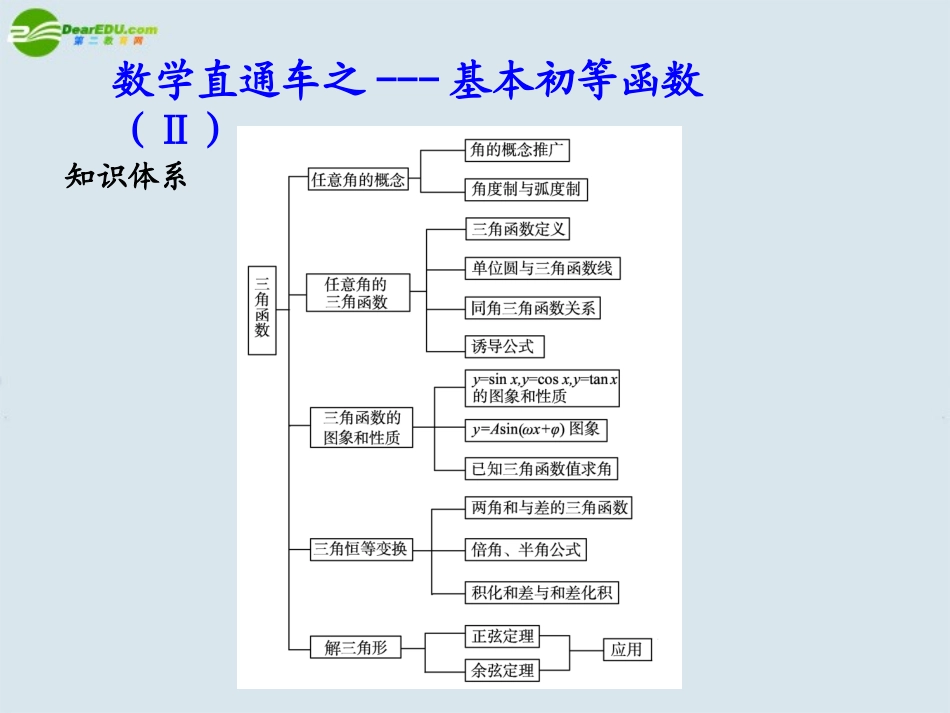
数学直通车之---基本初等函数（Ⅱ）知识体系第一节任意角与弧度制及任意角的三角函数基础梳理1.弧度制(1)弧AB的长=半径∠AOB=1弧度.rad=360°,1rad≈=.(2)扇形半径为r，圆心角的弧度数是α,则这个扇形的弧长l=|α|r,面积S=|α|,周长=|α|r+2r.2.角的概念的推广(1)任意角的定义角可以看成平面内一条射线所成的图形.2r1220'5718057.30绕着端点从一个位置旋转到另一个位置(2)按逆时针方向旋转形成的角叫做正角；按顺时针方向旋转形成的角叫做负角；一条射线没有作任何旋转形成的角叫做零角.(3)当角的顶点与坐标原点重合，角的始边与x轴的非负半轴重合，那么角的终边在第几象限，就称这个角是第几象限角.(4)所有与角α终边相同的角，连同角α在内，构成角的集合是{β|β=k·360°+α,k∈Z}.3.任意角的三角函数设α是一个任意角，α的终边上任意一点P的坐标是(x,y),它与原点的距离为r(r=),那么sinα=，cosα=,tanα=(x≠0).yrxryx22xy4.单位圆与三角函数线用单位圆中的有向线段表示三角函数（如图）.sinα=MP,cosα=OM,tanα=AT.典例分析题型一象限角问题【例1】若α是第二象限的角，则是第几象限的角?是第几象限的角?2α是第几象限的角?235.三角函数值在各象限的符号象限函数符号ⅠⅡⅢⅣsinα++--cosα+--+tanα+-+-分析由于α是第二象限的角，可以利用终边相同的角的表达式表示出α的范围，进而求得,,2α的范围，判定其所在的象限.23解由α是第二象限的角得k·360°+90°＜α＜k·360°+180°（k∈Z）.(1)k·180°+45°＜＜k·180°+90°（k∈Z）①当k=2n（n∈Z）时，n·360°+45°＜＜n·360°+90°（n∈Z）,则是第一象限角;②当k=2n+1（n∈Z）时，n·360°+225°＜＜n·360°+270°（n∈Z）,则是第三象限角.综合①、②可知，是第一或第三象限角.222222（2）·360°+30°＜＜·360°+60°（k∈Z）①当k=3n（n∈Z时）,n·360°+30°＜＜n·360°+60°（n∈Z）,则是第一象限角;②当k=3n+1（n∈Z）时，n·360°+150°＜＜n·360°+180°（n∈Z）,则是第二象限角；③当k=3n+2（n∈Z）时，n·360°+270°＜＜n·360°+300°（n∈Z）,则是第四象限角.综合①、②、③可知，是第一、第二或第四象限角.33333333k3k（3）2k·360°+180°＜2α＜2k·360°+360°（k∈Z）.故2α是第三、第四象限角或是终边落在y轴的负半轴上.举一反三1.设θ为第三象限角，试判断的符号.学后反思知道α所在的象限，则,，…所在的象限也可由象限等分法得到，下面以为例说明.如图所示，将每一个象限二等分（若是则三等分，……，）从x轴正向起按逆时针方向在各等分区域标上数字1，2，3，4，1，2，3，4；若α是第一象限角，则在标有数字1的区域内;若α是第二象限角，则在标有数字2的区域内，以此类推，则很容易确定所在的象限.3222232sin2cos2解析: θ为第三象限角，∴2kπ+π＜θ＜2kπ+(k∈Z),kπ+＜＜kπ+(k∈Z).当k=2n(n∈Z)时，2nπ+＜＜2nπ+（n∈Z）,此时在第二象限，∴sin＞0,cos＜0,∴＜0；当k=2n+1(n∈Z)时，(2n+1)π+＜＜(2n+1)π+(n∈Z),即2nπ+＜＜2nπ+(n∈Z),此时在第四象限，∴sin＜0,cos＞0,∴＜0.综上可知:＜0.3222342234222sin2cos222232742sin2cos2sin2cos22234题型二扇形弧长、面积公式的应用【例2】一个扇形的周长为20cm,当扇形的圆心角α等于多少弧度时，这个扇形的面积最大？并求出这个扇形的最大面积.分析运用扇形的面积公式和弧长公式建立函数关系，运用函数的性质来解决最值问题.学后反思求扇形最值的一般方法是根据扇形的面积公式，将其转化为关于半径（或圆心角）的函数表达式，进而求解.除此之外，也可直接设出两个参数，利用基本不等式求最值.解设扇形的半径为r，则弧长为l=20-2r,于是扇形的面积：S=(20-2r)r=-+25.当r=5时，l=10，α==2(弧度),S取到最大值，此时最大值为25.故当扇形的圆心角α=2弧度时，这个扇形的面积最大，最大面积是25.122(5)r1052cm2cm举一反三2.已知一扇形的圆心角是α,所在圆的半径为r.（1）若α=60°，r=10cm，求扇形的弧长及该弧所在的...