高二数学 2双曲线的简单几何性质课件 苏科版 课件VIP免费

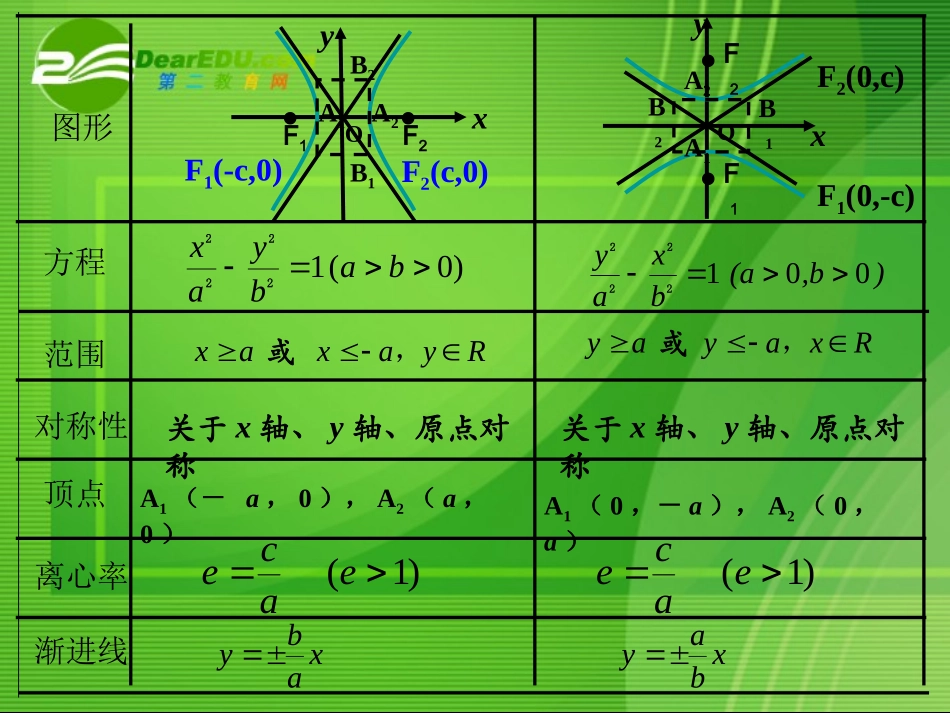
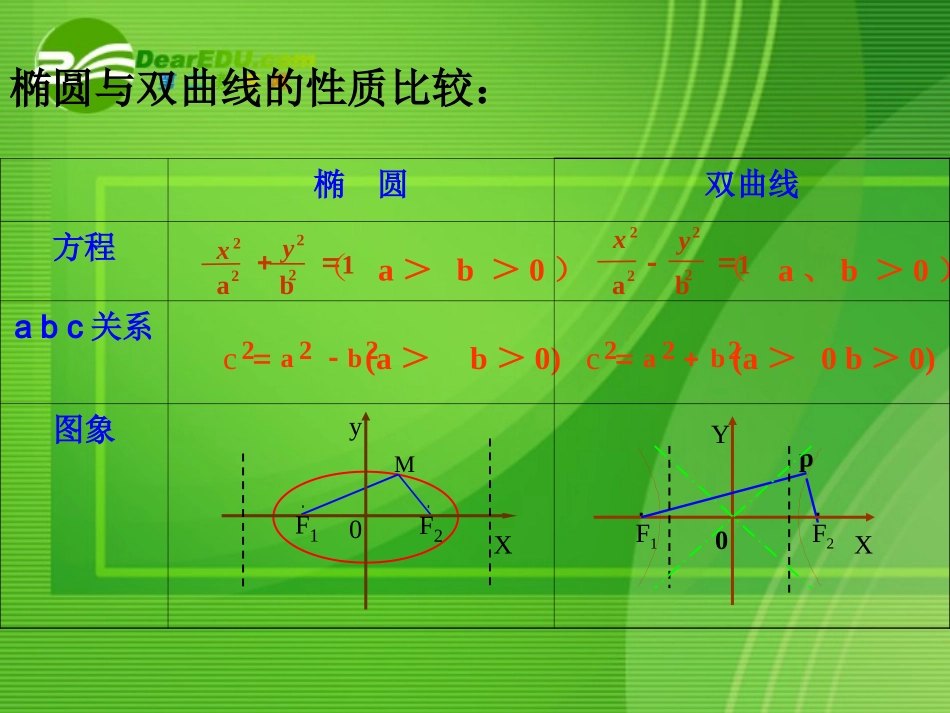
双曲线的双曲线的简单几何性质简单几何性质(2)(2)关于x轴、y轴、原点对称图形方程范围对称性顶点离心率)0(1babyax2222A1（－a，0），A2（a，0）A1（0，－a），A2（0，a）),b(abxay0012222Rxayay，或关于x轴、y轴、原点对称)1(eace渐进线xbay..yB2A1A2B1xOF2F1xB1yO.F2F1B2A1A2.F1(-c,0)F2(c,0)F2(0,c)F1(0,-c)Ryaxax，或)1(eacexaby12byax222（a＞b＞0）222ba(a＞0b＞0)c222ba(a＞b＞0)cyXF10F2MXY0F1F2p椭圆与双曲线的性质比较：12byax222（a、b＞0）椭圆双曲线方程abc关系图象渐近线离心率顶点对称性范围|x|a,|y|≤b|x|≥a，yR对称轴：x轴，y轴对称中心：原点对称轴：x轴，y轴对称中心：原点（-a,0)(a,0)(0,b)(0,-b)长轴：2a短轴：2b(-a,0)(a,0)实轴：2a虚轴：2be=ac(0＜e＜1)ace=(e1)无y=abx±yXF10F2MXY0F1F2p图象例2.求下列双曲线的渐近线方程，并画出图像：149).122yx149).222yx0xy如何记忆双曲线的渐进线方程？例1．已知双曲线的焦点在y轴上，焦距为16，离心率是4/3，求双曲线的标准方程。22222222(0)0.xyxyabab双曲线渐近线方程02222byax0))((byaxbyax或0byax.0byaxxaby＝能不能直接由双曲线方程推出渐近线方程？结论：100xy(a,b)ab2222双曲线方程中，把1改为0，得oxy例3．已知双曲线的渐近线是，并且双曲线过点02yx)3,4(M求双曲线方程.Q4M222222221ab1abxyyx设双曲线方程为？还是？oxy变形：已知双曲线渐近线是，并且双曲线过点02yx)5,4(N求双曲线方程.NQ22220,x;0,yxyab令双曲线为，若求得则双曲线的交点在轴若则焦点在轴上。222222221ab1abxyyx设双曲线方程为？还是？练习题：的双曲线方程。且过点有相同渐近线，求与)3,4(14.222Myx的双曲线方程。且焦点为有相同渐近线，求与)0,5(14.322yx方程。的焦点为顶点的双曲线，且以椭圆求渐近线为1521y.422yxx1.求下列双曲线的渐近线方程：328).122yx819).222yx4).322yx12549).422yx小结：.xaby1.12222＝的渐近线是byax知识要点：技法要点：22222222(0)0.xyxyabab双曲线渐近线方程22222.1yx.yxaabb的渐近线是＝