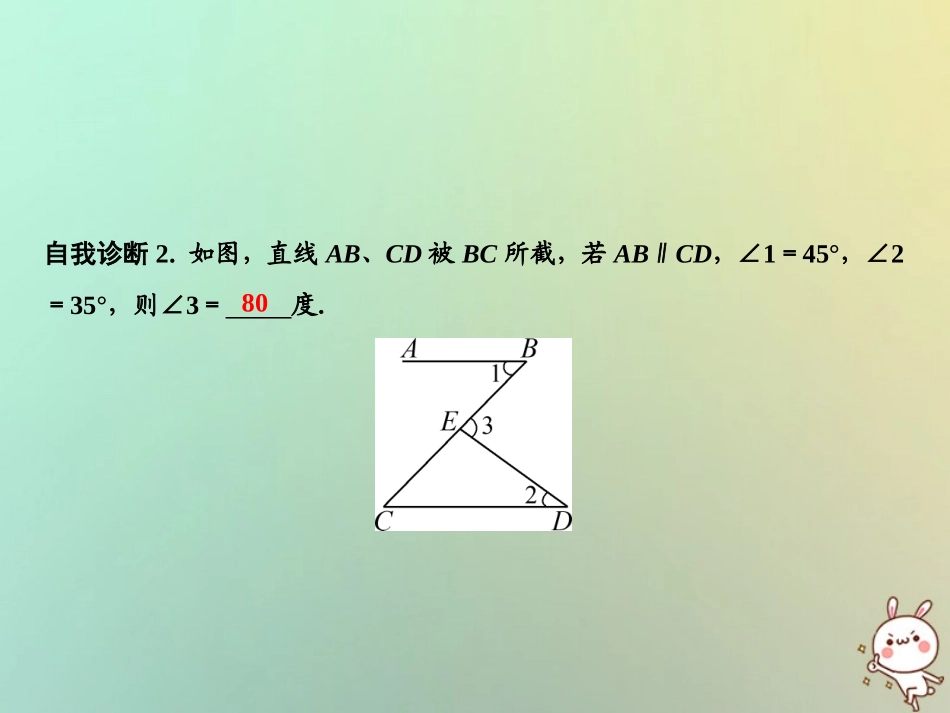
第十一章三角形11.2与三角形有关的角11.2.2三角形的外角2018秋季数学八年级上册•R三角形的外角性质三角形的外角等于与它的两个内角的和.自我诊断1.(黔东南中考)如图,∠ACD=120°,∠B=20°,则∠A的度数是()A.120°B.90°C.100°D.30°易错点:在运用三角形的外角性质时,忽略“不相邻”的条件.不相邻C自我诊断2.如图,直线AB、CD被BC所截,若AB∥CD,∠1=45°,∠2=35°,则∠3=度.801.如图,已知AB∥CD,∠C=65°,∠E=30°,则∠A的度数为()A.30°B.32.5°C.35°D.37.5°2.把一副三角板按如图所示的方式放置,则两条斜边所形成的钝角∠α=度.C1653.一个零件的形状如图所示,按规定∠A应等于90°,∠B、∠C应分别是21°和32°,检验员量得∠BDC=148°,就断定这个零件不合格,这是为什么?解:不合格.延长CD交AB于E,则∠CEB=∠C+∠A=90°+32°=122°,又∵∠CDB是△DBE的外角,∴∠CDB=122°+21°=143°≠148°,∴不合格.4.如图,图中是△ABC的外角的是()A.∠EAB和∠EADB.∠EAD和∠DACC.∠EAB和∠EAD、∠DACD.以上说法都不对D5.等腰三角形的一个外角为110°,则它的底角为()A.55°B.70°C.55°或70°D.以上都不对6.如图,在△ABC中,∠A=50°,∠ABC=70°,BD平分∠ABC,则∠BDC的度数是.C85°7.如图,在△ABC中,∠A=60°,∠1=20°,∠2=25°.求∠BOC.解:延长BO交AC于D;利用外角可求∠BOC=105°.8.如图所示,已知在△ABC中,∠ABC和∠ACB的外角平分线相交于点P.(1)若∠ABC=30°,∠ACB=70°,求∠BPC的度数;(2)若∠ABC=α,∠BPC=β,求∠ACB度数.解:(1)∠BPC=180°-(12∠EBC+12∠BCF)=180°-12(∠EBC+∠BCF)=180°-12(180°-∠ABC+180°-∠ACB)=12(∠ABC+∠ACB)=50°;(2)由(1)知,∠BPC=12(∠ABC+∠ACB),∵∠BPC=β,∠ABC=α,∴β=12(α+∠ACB).故∠ACB=2β-α.