高中数学 123 同角三角函数的基本关系式课件 新人教B版必修4 课件VIP免费

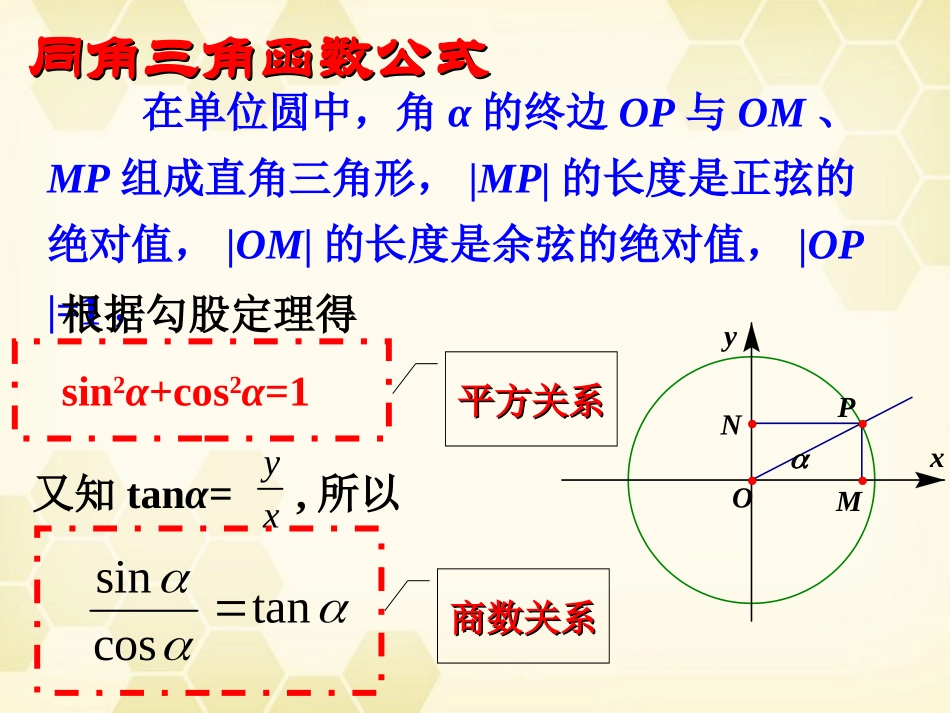
1.2.31.2.3同角三角函数关系式同角三角函数关系式在单位圆中，角α的终边OP与OM、MP组成直角三角形，|MP|的长度是正弦的绝对值，|OM|的长度是余弦的绝对值，|OP|=1，根据勾股定理得sin2α+cos2α=1NMPyxO又知tanα=,所以yxtancossin平方关系平方关系商数关系商数关系同角三角函数公式同角三角函数公式注意：1.公式中的角一定是同角，否则公式可能不成立.如sin230º+cos260º≠1.2.同角不要拘泥于形式α，，6α等等都可以.2如sin24α+cos24α=1.3.商数关系中注意限制条件.即cosα≠0.α≠kπ+，kZ.∈2(1)给定角的一个三角函数值，求这个角的其余三角函数值。应用：(2)化简三角函数式和证明三角恒等式。应用的方法：正用,逆用、变形用.22sin1cos22cos1sinsincostansincostan2221costancos222sintan1sin例1已知，并且α是第二象限角，求α的余弦和正切值．54sin解：∵sin2α+cos2α=1，α是第二象限角.2243cos1sin1(),55cos0345354cossintan例2．已知，求sinα、tanα的值.178cos解：∵cosα＜0∴α是第二或第三象限角．（ⅰ）当α是第二象限角时，22815sin1cos1(),171715sin1517tan.8cos817（ⅱ）当α是第三象限角时，15sin,1715tan.8例3.已知sinα－cosα=,180º<α<270º.求tanα的值。55解：以题意和基本三角恒等式，得到方程组225sincos5sincos1消去sinα，得5cos2α－cosα－2=0，5由方程解得cosα=255或cosα=55因为180º<α<270º，所以cosα<0，即cosα=55代入原方程组得sinα=255于是tanα==2.sincos例4化简：440sin12解：原式=221sin(36080)1sin802cos80cos80例5化简：1tancossin解：原式=sincossin1cossincossincoscos=cosθ.化简方向：化简方向：切化弦切化弦例6已知tanθ=2求值：sincos(1)2sin3cos解：（1)分子分母同除以cosθ原式=tan12tan3=1/7.化简方向：化简方向：弦化切弦化切221(2)sincos（2)分子“1”换为“sin2θ+cos2θ”原式=2222sincossincos=5/3.22tan1tan1例7.求证：(1)sin4α－cos4α=2sin2α－1；证明：左边=(sin2α+cos2α)(sin2α－cos2α)=sin2α－cos2α=sin2α－(1－sin2α)=2sin2α－1右边.所以原等式成立.(2)2222sintansintan证明：原式右边=tan2α(1－cos2α)=tan2α－tan2αcos2α2222sintancoscos=tan2α－sin2α=左边.(3)cos1sin1sincos证明：左边coscos(1sin)cosxxxx=右边∴原等式成立.1sincosxx21sin(1sin)cosxxx证明等式的常用方法：1.从等式的一边证得它等于另一边；2.先证明另外一个等式成立，从而推出需要证明的等式成立；3.利用作差(作商)的方法。