高考数学 基本初等函数 专题复习课件VIP免费

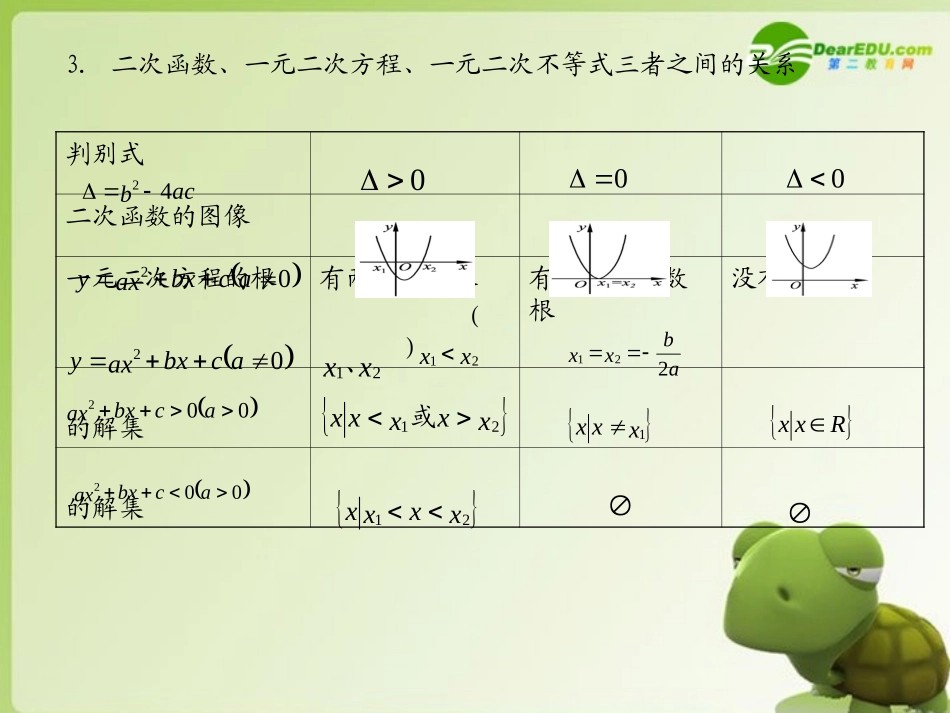
第三单元基础初等函数yy12xx12第一节一次函数、二次函数基础梳理1.一次函数的性质与图象(1)函数叫做一次函数.它的定义域为R,值域为R.(2)一次函数具有如下一些主要性质:①函数值的改变量与自变量的改变量的比值等于常数k;②当k>0时,一次函数是;当k<0时,一次函数是;③当b=0时,一次函数变为函数,是奇函数;当b≠0时,它既不是,又不是;④直线y=kx+b与x轴的交点为,与y轴的交点为y=kx+b(k≠0)增函数减函数正比例奇函数偶函数(0,b)0,kb2.二次函数的性质与图象(1)函数叫做二次函数,它的定义域是(2)二次函数有如下性质:①函数的图象是,抛物线顶点的坐标是,抛物线的对称轴是;②当a>0时,抛物线开口向上,函数在处取;在区间上是减函数,在上是增函数;③当a<0时,抛物线开口,函数在处取最大值;在区间上是增函数,在上是减函数;④与y轴的交点是⑤当Δ=b2-4ac>0时,与x轴两交点的横坐标分别是方程a的的两根;当Δ=0时,与x轴切于一点;当Δ<0时,与x轴;⑥当b≠0时,是非奇非偶函数；当b=0时,是;⑦对于函数f(x),若对任意自变量x的值,都有f(a+x)=f(a-x),则f(x)的图象关于直线对称.02acbxaxyR.一条抛物线abacab44,22abx2最小值ab2,,2ab向下(0,c)xx21、0,2ab没有交点偶函数x=aabx2abx2abf2abf2ab2,,2ab02acbxaxy3.二次函数、一元二次方程、一元二次不等式三者之间的关系判别式二次函数的图像一元二次方程的根有两相异实根（）有两相等实数根没有实数根的解集的解集acb4200002acbxaxy02acbxaxy002acbxax002acbxaxxx21、xx21xxxxx21或xxxx21abxx221xxx1Rxx4.二次函数在闭区间上的最值问题y=f(x)=a+k(a>0)在[m,n]上的最值问题.(1)h∈[m,n]时,=k,=max{f(m),f(n)}；(2)h[m,n]时,当hn时,f(x)在[m,n]上单调递减,=,=.hx2yminymaxyminymaxymaxymin递增f(m)f(m)f(n)f(n)典例分析题型一一次函数性质的应用【例1】一次函数y=(m+2)x+2m-1是增函数,且它的图象与y轴的交点在x轴的下方,求实数m的取值范围.分析当k>0时，y=kx+b(k≠0)为增函数,其图象与y轴的交点为(0,b).解 y=(m+2)x+2m-1是增函数,∴m+2>0.①又 函数y=(m+2)x+2m-1的图象与y轴的交点在x轴下方,∴2m-1<0.②由①、②解得-20时,函数图象是上升的;k<0时,函数图象是下降的.b反映了函数图象与y轴交点的位置,b>0时,交于x轴上方;b=0时,交于原点;b<0时,交于x轴下方.b又叫做直线y=kx+b在y轴上的截距.举一反三1.已知函数y=(2m-1)x+1-3m,m为何值时：(1)这个函数为一次函数?(2)函数值y随x的增大而减小?(3)这个函数图象与直线y=x+1的交点在x轴上?解析:(1)当m≠时,这个函数为一次函数.(2)根据一次函数的性质,可知当2m-1<0,即m<时,y随x的增大而减小.(3)直线y=x+1与x轴交于点(-1,0),将其代入y=(2m-1)x+1-3m中,得1-2m+1-3m=0,∴m=.212152题型二二次函数图像和性质的应用【例2】已知二次函数f(x)满足f(2)=-1,f(-1)=-1,且f(x)的最大值是8,试确定此二次函数.分析由题目条件知二次函数过(2,-1),(-1,-1)两点,且知其最大值,所以可应用一般式、顶点式或两根式解题.解方法一:利用二次函数一般式.设f(x)=a+bx+c(a≠0).由题意得,解得∴所求二次函数为y=-4+4x+7.方法二:利用二次函数的顶点式.设f(x)=a+n(a≠0). f(2)=f(-1),x284411242abaccbacba744cbax2mx2∴抛物线对称轴为x=，∴m=.又根据题意函数有最大值y=8,∴y=f(x)=a+8. f(2)=-1,∴a+8=-1，解得a=-4.∴f(x)=-4+8=-4+4x+7.方法三:利用二次函数的两根式.由已知f(x)+1=0的两根为=2,=-1,故可设f(x)+1=a(x-2)(x+1)(a≠0),即f(x)=a-ax-2a-1.又函数有最大值=8,即=8,解得a=-4或a=0(舍去).∴所求函数解析式为f(x)=-4+4x+7.2121221...