高中数学 同角三角函数的基本关系课件 新人教A版必修4 课件VIP免费

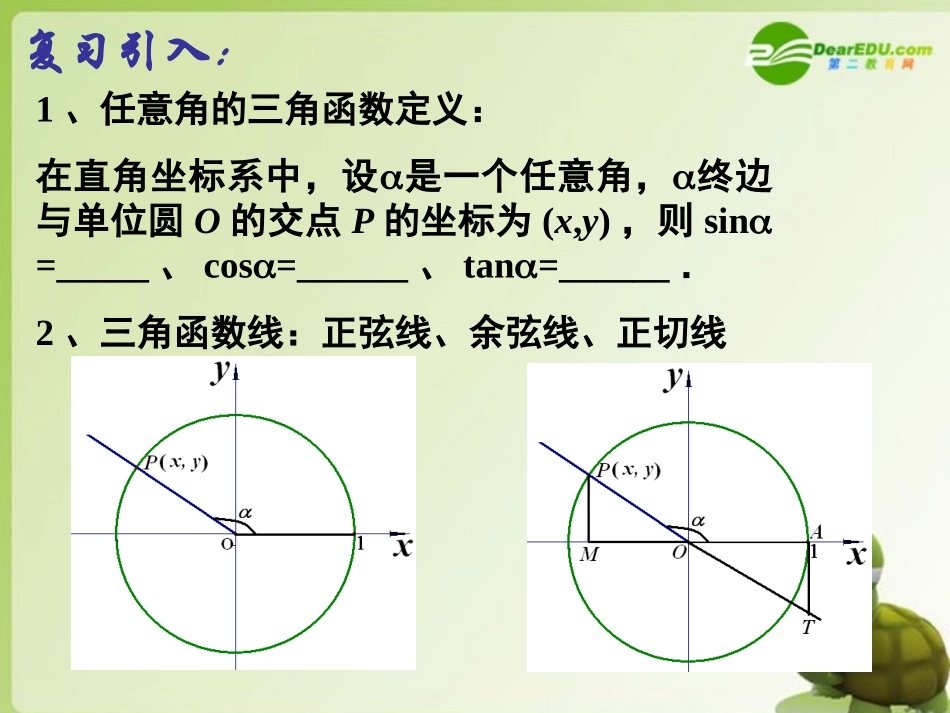
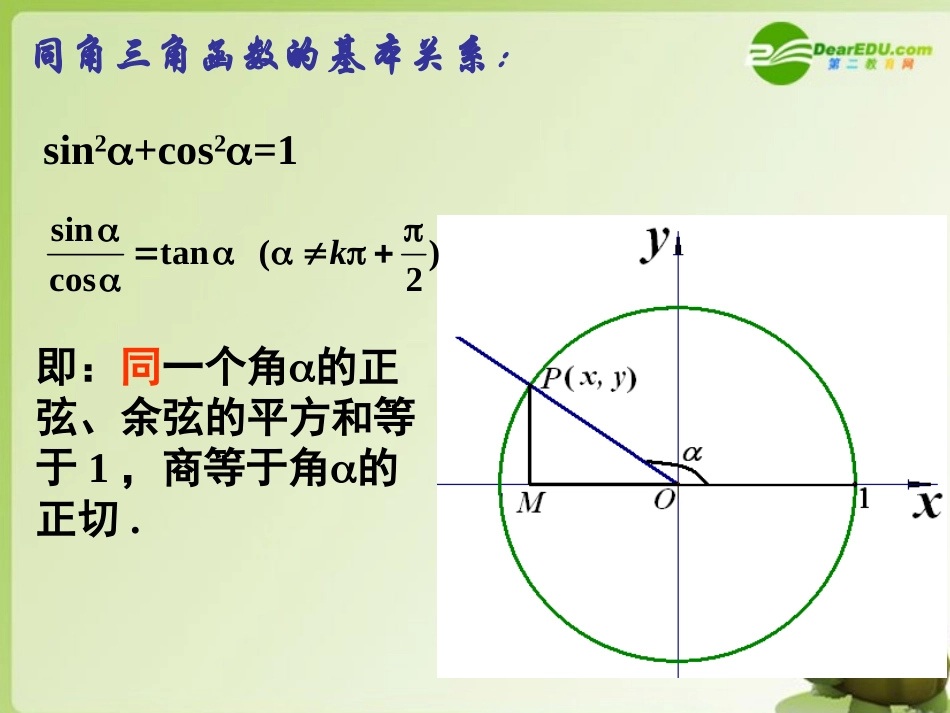
缪荷芳复习引入：1、任意角的三角函数定义：在直角坐标系中，设是一个任意角，终边与单位圆O的交点P的坐标为(x,y)，则sin=_____、cos=______、tan=______．2、三角函数线：正弦线、余弦线、正切线同角三角函数的基本关系：sin2+cos2=1)2(tancossink即：同一个角的正弦、余弦的平方和等于1，商等于角的正切.例题与练习：._____cos_____sin2tan3.____tan_____sin54cos2.tancos1312sin11，，则）已知（，，则）已知（的值、求是第二象限角，，且）已知、（由此例可以看出，就是sin2+cos2=1的一个变形，你能利用同角三角函数的基本关系推导出更多的关系式吗？xxxxcossin1sin1cos.cossin1sin1cos2xxxx、求证：是第二象限角）（其中）（；））（（、化简下列各式：sin1sin1sin1sin12costan11322.cos9sin4cos3sin22tan4值，求、已知xxxxx的值；，求变式一：已知xxxxx2222cos9sin4cos3sin22tan的值；，求变式二：已知xxxxcossincos12tan2变式三：已知tanx=2，求cos2x+sinx·cosx的值.小结已知sin+cos=，求下列各式的值：（1）sin-cos；（2）sin3+cos3.51思考：sintancos公式运用已知一个角的一个三角函数值，求这个角的其它几个三角函数值。sincostan22sincos12tansintan121costan1符号与cos同符号与cos同