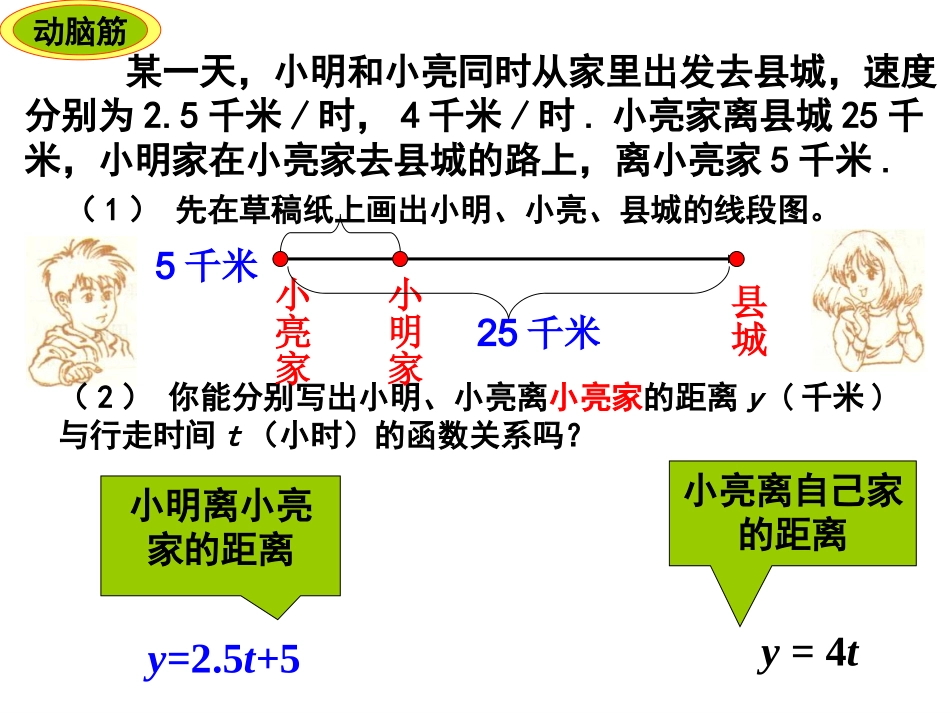
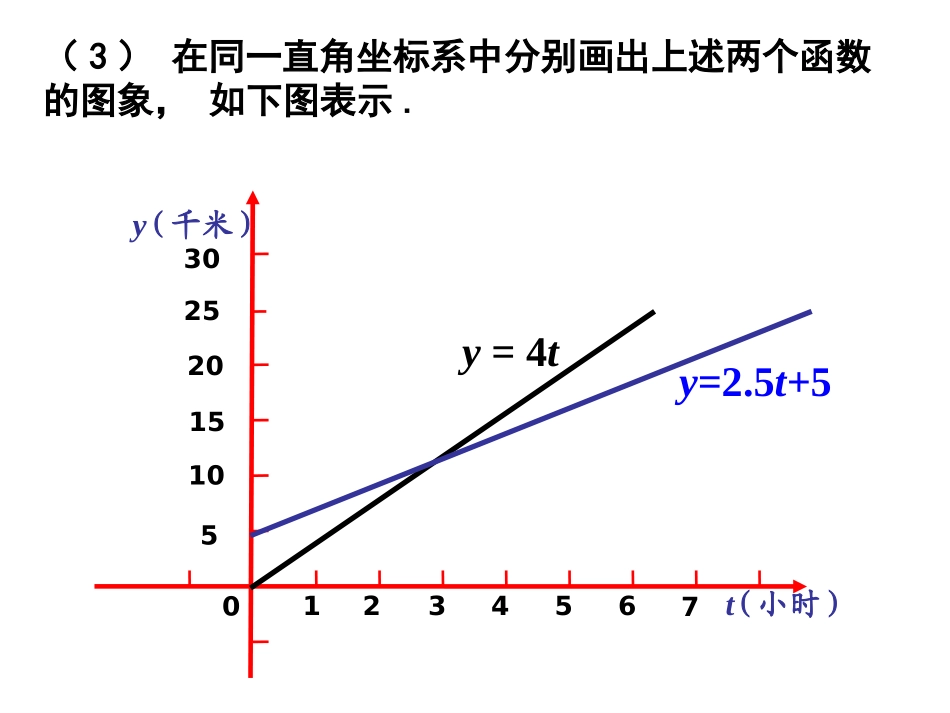
建立一次函数模型建立一次函数模型(4)(4)动脑筋某一天,小明和小亮同时从家里出发去县城,速度分别为2.5千米/时,4千米/时.小亮家离县城25千米,小明家在小亮家去县城的路上,离小亮家5千米.(2)你能分别写出小明、小亮离小亮家的距离y(千米)与行走时间t(小时)的函数关系吗?小明离小亮家的距离小亮离自己家的距离(1)先在草稿纸上画出小明、小亮、县城的线段图。小亮家县城小明家y=2.5t+5y=4t25千米5千米(3)在同一直角坐标系中分别画出上述两个函数的图象,如下图表示.t(小时)y(千米)5101520253012345670y=4ty=2.5t+5(4)你能从图中看出,在出发后几个小时小亮追上小明吗?t(小时)y(千米)5101520253012345670y=4ty=2.5t+5p两条段线的交点P的横坐标约为3.3,因此在出发后约3.3小时,小亮追上了小明.上述例子的问题中,小亮追上小明的时间是所绘直角坐标系中两条线段y=2.5t+5与y=4t的交点P的横坐标,而交点P的坐标是下述二元一次方程组的解:2.554ytyt上述例子就是通过在同一个直角坐标系中,分别画出y=2.5t+5与y=4t的图象,求出交点坐标,从而得出二元一次方程组的近似值.这种解二元一次方程组的方法叫做图像法.t(小时)y(千米)5101520253012345670My=4ty=2.5t+5(5)你能从图中看出,谁先到达县城吗?如图所示,过M(0,25)作射线l与x轴平行,它先与射线y=4t相交,这表明小亮先到达县城.例1:用图像法解方程组:x+y=1(1)x-y=3(2){2、在同一平面直角坐标系中,画出下列函数的图象.(1)y=-x+1;(2)y=x-3并观察两条直线的交点,说出交点坐标.{x=2y=-1易知1、将二元一次方程变形为一次函数形式:由方程(1)得:y=-x+1由方程(2)得:y=x-3y=-x+1y=x-3∧y﹥642-2-4-10-5510x642-2-4-10-5510642-2-4-10-5510(2,-1)o1.图象法解二元一次方程组的步骤:(1)将二元一次方程化为一次函数形式;(2)在同一平面直角坐标系中画出函数图象;(3)利用图象交点确定二元一次方程组的解.yx-20-11-10-9-8-7-6-5-4-3-1-112365421-2-3yx-20-11-10-9-8-7-6-5-4-3-1-112365421-2-3yx-20-11-10-9-8-7-6-5-4-3-1-112365421-2-3练习1、用图象法求下述二元一次方程组的解:x+y=22x-y=10{解:由(1),得y=-x+2由(2),得y=2x-10在同一平面直角坐标系中,分别画出函数y=-x+2与y=2x-10的图象,即原方程组的解是x=4y=-2{y=-x+2y=2x-10(4,-2)它们的交点坐标(4,-2)就是原方程组的解.练习2、用图象法求下述二元一次方程组的近似解.347.624.4xyxy图象法解二元一次方程组的基本步骤课本P.55A组第六题.每课必练:P29T9和T10