高中数学选修2-2数学归纳法ppt 课件VIP免费

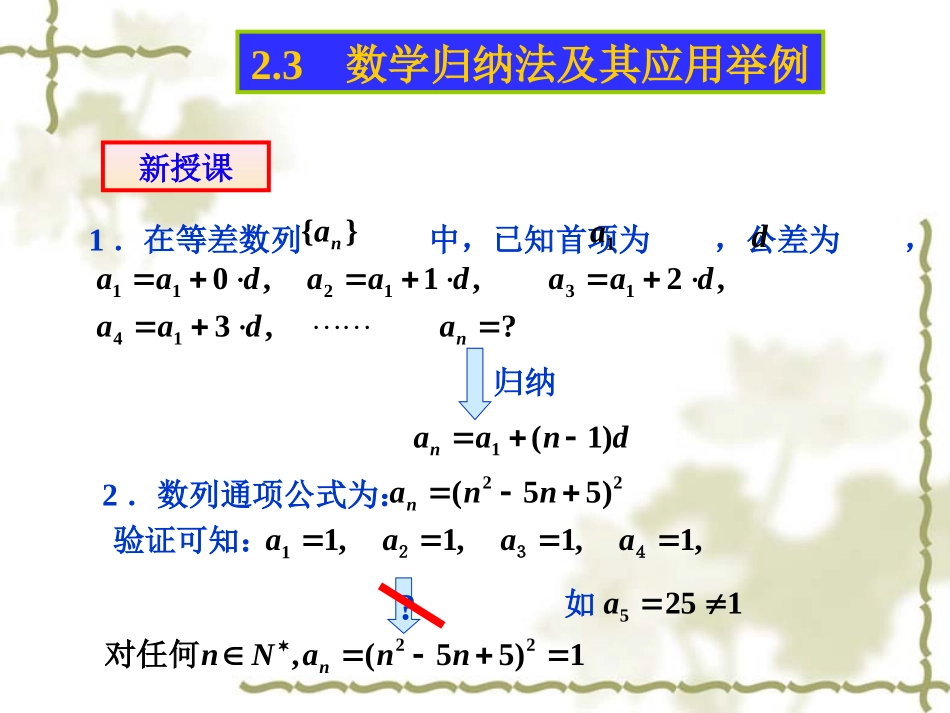
2.32.3数学归纳法数学归纳法2.3数学归纳法及其应用举例课题引入①观察：6＝3＋3，8＝5＋3，10＝3＋7，12＝5＋7，14＝3＋11，16＝5＋11，···78＝67＋11，···我们能得出什么结论？任何一个大于等于6的偶数，都可以表示成两个奇质数之和．②教师根据成绩单，逐一核实后下结论：“全班及格”．由一系列有限的特殊事例得出一般结论的推理方法，通常叫做归纳法．不完全归纳法完全归纳法这两种下结论的方法都是由特殊到一般，这种推理方法叫归纳法．归纳法是否能保证结论正确?(1)是不完全归纳法，有利于发现问题，形成猜想，但结论不一定正确．(2)是完全归纳法，结论可靠，但一一核对困难．1)55(,22nnaNnn对任何?2.3数学归纳法及其应用举例新授课1．在等差数列中，已知首项为，公差为，}{na1ad,2,1,0131211daadaadaa?,314nadaadnaan)1(1归纳22)55(nnan2．数列通项公式为：验证可知：,1,1,1,11４３２aaaa1255a如2.3数学归纳法及其应用举例新授课对于由不完全归纳法得到的某些与自然数有关的数学命题我们常采用下面的方法来证明它们的正确性：先证明当n取第一个值n0(例如n0=1)时命题成立，然后假设当n=k(kN,k≥∈n0)时命题成立证明当n=k+1时命题也成立，这种证明方法叫做数学归纳法.数学归纳法的两个步骤：()Ⅰ证明当n＝n0(n＝1)(如n＝1或2等)时，结论正确；()Ⅱ假设n＝k(kN*∈且k≥n0)时结论正确，并应用此假设证明n＝k＋1时结论也正确．注意:运用数学归纳法证题,以上两步缺一不可定义2.3数学归纳法及其应用举例新授课dnaan)1(1如果是等差数列，已知首项为，公差为，那么}{na1ad对一切都成立．Nn证明：（1）当n=1时，,1a左边,011ada右边等式是成立的．（2）假设当n=k时等式成立，就是,)1(1dkaak那么daakk1dkaddka]1)1[(])1([11这就是说，当n=k+1时，等式也成立由（1）和（2），可知的等式对任何都成立．Nn2.3数学归纳法及其应用举例新授课数学归纳法证明一个与正整数有关命题的步骤是：（1）证明当取第一个值（如或2等）时结论正确；10nn0n（2）假设时结论正确，证明时结论也正确．)N(0nkkkn且1kn递推基础递推依据小时候学数数的经历：先会数1，2，3；再数到10；再数到20以内的数再数到30以内的数……，终于有一天我们可以骄傲地说：我什么数都会数了，为什么呢?因为会数1，2，3……有了数数的基础,会在前一个数的基础上加班1得到后一个数，进行传递，所以，可以说什么数都会数了．“找准起点，奠基要稳”“用上假设，递推才真”例题1用数学归纳法证明6)12)(1(3212222nnnn证明：（1）当n=1时，左边＝12＝1，右边＝等式成立。（2）假设当n=k时，等式成立，就是163216)12)(1(3212222kkkk那么61)1(21)1()1(6)32)(2)(1(6)672)(1(6)1(6)12)(1()1(6)12)(1()1(32122222222kkkkkkkkkkkkkkkkkkk这就是说，当n=k+1时等式也成立。根据（1）和（2），可知等式对任何nN∈＊都成立。2.3数学归纳法及其应用举例例题讲解例2用数学归纳法证明.)12(5312nn【分析】(2)第一步应做什么?本题的n0应取多少?n0=1,211（3）在证传递性时，假设什么？求证什么?假设1+3+5+…..+（2k-1）=k2求证1+3+5十….十(2k-1)十(2k+1)=(k+1)2（4）怎样将假设1+3+5+…..+（2k-1）=k2推理变形为1+3+5十….十(2k-1)十(2k+1)=(k+1)22.3数学归纳法及其应用举例例题讲解例2用数学归纳法证明.)12(5312nn证明：（1）当n=1时，左边=1，右边=1，等式成立．（2）假设当时，等式成立，就是kn.)12(5312kk那么222)1(12]1)1(2[(]1)1(2[)12(531kkkkkkk这就是说，当n=k+1时，等式也成立．由（1）和（2），可知的等式对任何都成立．Nn1、用数学归纳法证明：1+2+3+…+n=n(n+1)/2(nN)∈；证明:(1)当n=1时,左边=1,右边=1,等式是成立的。(2)假设当n=k时等式成立，就是1+2+3+…+k=k(k+1)/2那么，1+2+3+…+k+(k...