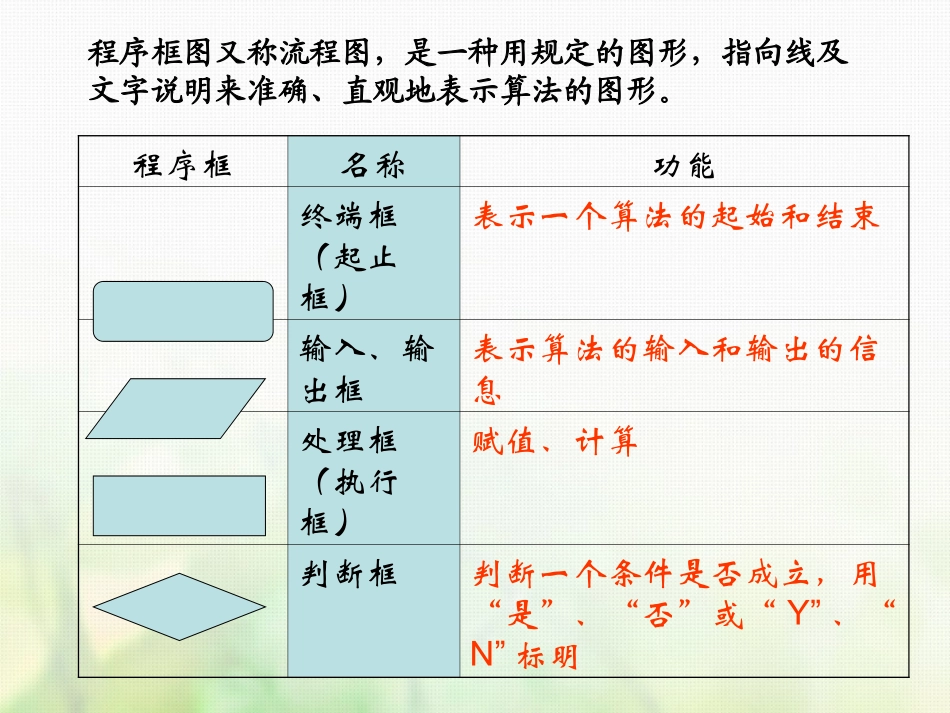
§1.1.2.2算法的基本逻辑结构算法初步程序框图又称流程图,是一种用规定的图形,指向线及文字说明来准确、直观地表示算法的图形。程序框名称功能终端框(起止框)表示一个算法的起始和结束输入、输出框表示算法的输入和输出的信息处理框(执行框)赋值、计算判断框判断一个条件是否成立,用“是”、“否”或“Y”、“N”标明新课讲解:算法的三种基本逻辑结构:1.顺序结构2.条件结构3.循环结构开始输入n求n除以ii的余数i的值增加1,仍用i表示i>n-1或r=0?r=0?n不是质数n是质数结束否否是是i=2顺序结构输入ni=2由若干个依次执行的处理步骤组成的。条件结构r=0?n不是质数n是质数结束是否算法的流程根据条件是否成立有不同的流向。循环结构i的值增加1,仍用i表示i>n-1或r=0?否是是求n除以i的余数r在一些算法中,从否处开始,按照一定条件,反复执行某一处理步骤的情况,这就是循环结构。反复执行的处理步骤称为循环体。(1)顺序结构顺序结构是最简单的算法结构,语句与语句之间,框与框之间是按从上到下的顺序进行的,它是由若干个依次执行的处理步骤组成的,它是任何一个算法都离不开的一种基本算法结构。顺序结构在程序框图中的体现就是用流程线将程序框自上而下地连接起来,按顺序执行算法步骤。步骤n步骤n+1例3、已知一个三角形的三边分别为a、b、c,利用海伦公式设计一个算法,求出它的面积,并画出算法的程序框图。算法步骤:(自然语言)第一步,输入三角形三条边的边长a,b,c.第二步,计算p=.第三步,计算S=a+b+c2.p(p-a)(p-b)(p-c)第四步,输出S.开始输入a,b,c结束p=a+b+c2S=.p(p-a)(p-b)(p-c)输出S算法步骤:(自然语言)第一步,输入三角形三条边的边长a,b,c.第二步,计算p=.第三步,计算S=第四步,输出S.(2)条件结构在一个算法中,经常会遇到一些条件的判断,算法的流程根据条件是否成立有不同的流向.条件结构就是处理这种过程的结构.分类是算法中经常发生的事情,条件结构的主要作用就是表示分类.条件结构可用程序框图表示为下面两种形式.步骤A步骤B满足条件?否是步骤A满足条件?否是例4任意给定3个正实数,设计一个算法,判断分别以这3个数为三边边长的三角形是否存在.画出这个算法的程序框图.开始输入a,b,ca+b>c,a+c>b,b+c>a是否同时成立?存在这样的三角形不存在这样的三角形结束否是条件结构算法步骤如下:第一步,输入3个正实数a,b,c.第二步,判断a+b>c,a+c>b,b+c>a是否同时成立.若是,则存在这样的三角形;否则,不存这样的三角形.输入a,b,c存在这样的三角形否是条件结构不存在这样的三角形c+a>b?b+c>a?a+b>c?是是开始结束否否例4设计一个求解一元二次方程算法步骤:第一步,输入a,b,c.第二步,计算判别式Δ=b2-4ac.第三步,判断Δ≥0是否成立.若是,则计算p,q的值.否则,输出“方程没有实数根”,结束算法.开始输入a,b,cΔ=b2-4acx1=p+qx2=p-qΔ≥0?Δ=0?输出x1,x2输出p方程无实数根结束是否是否的算法,并画出程序框图表示.02cbxax2qa第四步,判断Δ=0是否成立.若是,则输出12;xxp否则,计算两根并输出.2bpa开始输入a,b,cΔ=-4acΔ≥0?Δ=0?输出,结束方程无实数根输出x1x2b2ba22bxa1x2x2bxa否是是否例4程序框图也可设计为输入系数a,b,c输出X1、X2计算acb42计算abx21abx22开始结束设计算法,求一元二次方程ax2+bx+c=0()的根,画出相应的流程图a≠0输出x1,x2输出x1,x2输入系数a,b,c△<0?12bbx,x2a2a否是输出无实数解计算acb42开始结束(3)循环结构循环结构指的是按照一定的条件反复执行的某些算法步骤.反复执行的步骤称为循环体.循环体满足条件?否是循环体满足条件?否是执行一次循环体后,对条件进行判断,如果条件不满足,就继续执行循环体,直到条件满足时终止循环.在每次执行循环体前,对条件进行判断,当条件满足,执行循环体,否则终止循环.例5设计一个计算1+2+3+…+100的值的算法,并画出程序框图.第1步,0+1=1.第2步,1+2=3.第3步,3+3=6.第4步,6+4=10.……第100步,4950+100=5050.算法2:第一步,令i=1,S=0.第二步,若i...