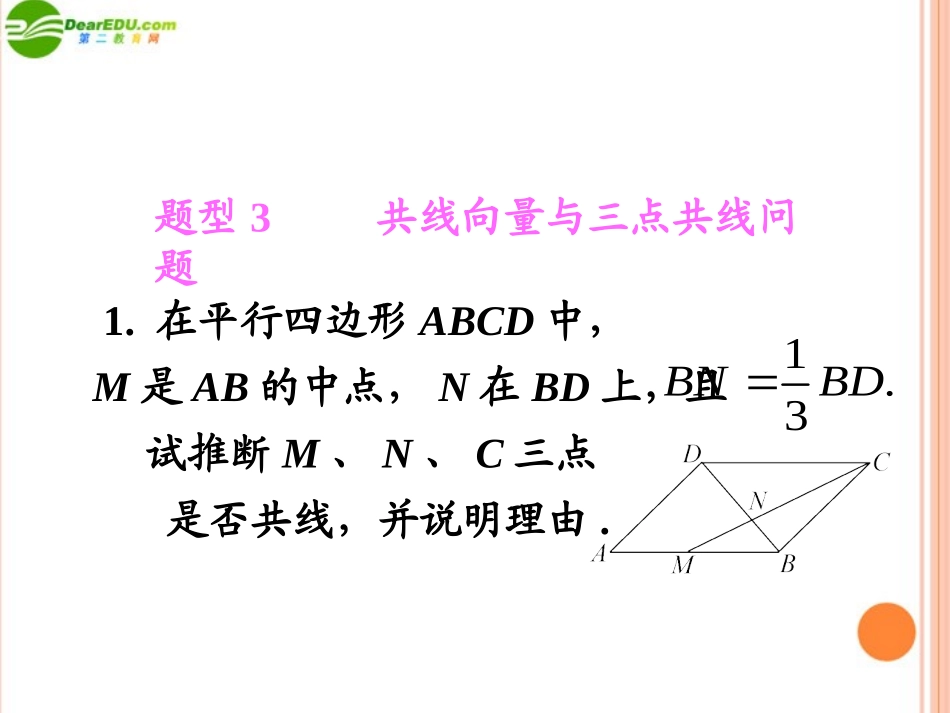
第五章平面向量第讲(第二课时)题型3共线向量与三点共线问题1.在平行四边形ABCD中,M是AB的中点,N在BD上,且试推断M、N、C三点是否共线,并说明理由.1.3BNBD解:因为所以所以向量与共线,故M、N、C三点共线.点评:用向量法证明几何中的平行或共线问题,就是用向量表示图中的有关线段,利用向量的相等得到线线平行或多点共线,如本题中的三点共线,即从这三点中任取两点构成向量,然后看这两个向量是否是共线向量.1,2MCMBBCABAD�11MN=MB+BN=AB+BD2311111(-)(),23323ABADABABADMC��MN�MC�设E、F分别是四边形ABCD的对角线AC、BD的中点,试推断向量与是否共线.EF�ABCD�,EFEAABBF�,EFECCDDF�2()()().EFEAECABCDBFDF�0,0.EAECBFDF�2,ABCDEF�EF�ABCD�解:因为又所以因为E、F分别是AC、BD的中点,所以所以故与共线.2.如图,三角形ABC中,点M是BC的中点,点N在边AC上,AM与BN相交于点P,设=e1,=e2.试用e1、e2表示.解:因为=e1,=e2,则又所以题型4平面向量基本定理的应用2,ANNC�AB�AC�AP�AB�AC�121(),2AMee�2,ANNC�22.3ANe�又设则由得所以解得所以12212(),(-)-,23kAPAMeeBPkBNkANABeke�,APABBP�121212()-,23keeeeke1-2,223kk45,35k1222.55APee�点评:本题向量比较多,一般取不共线的两向量作为基本向量,其他向量都往这两个向量转化,如本题中尽量往△ABC的边所在向量上转化,转化的策略是利用加减法运算合并向量或分解向量.ABAC�、在平行四边形ABCD中,M、N分别是CD、BC的中点,设试以a、b为基底表示向量和.AMaANb�,,AB�AD�.ABBNANADDMAM�,1,21.2ABADbADABa��42-,3342-.33ABbaADab��解:由图知,所以解得3.O是平面内一定点,A、B、C是平面内不共线的三个点,动点P满足λ∈[0,+∞),则点P的轨迹一定通过△ABC的()A.外心B.内心C.重心D.垂心题型5向量的几何运算(),||||ABACOPOAABAC���B解:由已知得因为与是单位向量,所以是以这两个单位向量为邻边的平行四边形的对角线所在向量,从而点P在∠BAC的平分线上,故选B.点评:有关向量的几何运算,是数形结合的一个方面,正确理解运算法则是基础,掌握运算规律是重点,而综合应用则是考点、难点与关键.().||||ABACAPABAC���||ABAB��||ACAC��||||ABACABAC��O是平面ABC内一点,且则三角形ABC一定是()A.直角三角形B.等腰三角形C.等边三角形D.斜三角形(-2)0,OBOCOACB�-2(-)(-),OBOCOAOBOAOCOAABAC�-,CBABAC�22-0,ABAC�||||,ABAC�B解:由而可得即有所以三角形ABC是等腰三角形,故选B.1.关于实数与向量的积(1)向量本身具有“形”和“数”的双重特点,而在实数与向量的积的运算过程中既要考虑模的大小,又要考虑方向,因此它是数形结合思想的具体运用,这点提示我们解题时不要脱离了向量的几何意义.(2)对任意非零向量a,是一个单位向量.||aa(3)设(x,y∈R),则P、A、B三点共线的充要条件是x+y=1.2.向量是一个几何量,是有“形”的量,因此,在研究向量的有关问题时,一定要结合图形进行分析、判断、求解,这是研究平面向量最重要的方法与技巧.OPxOAyOB�