高考数学第1轮总复习 全国统编教材 12.3函数的极限与连续性课件 理 课件VIP免费

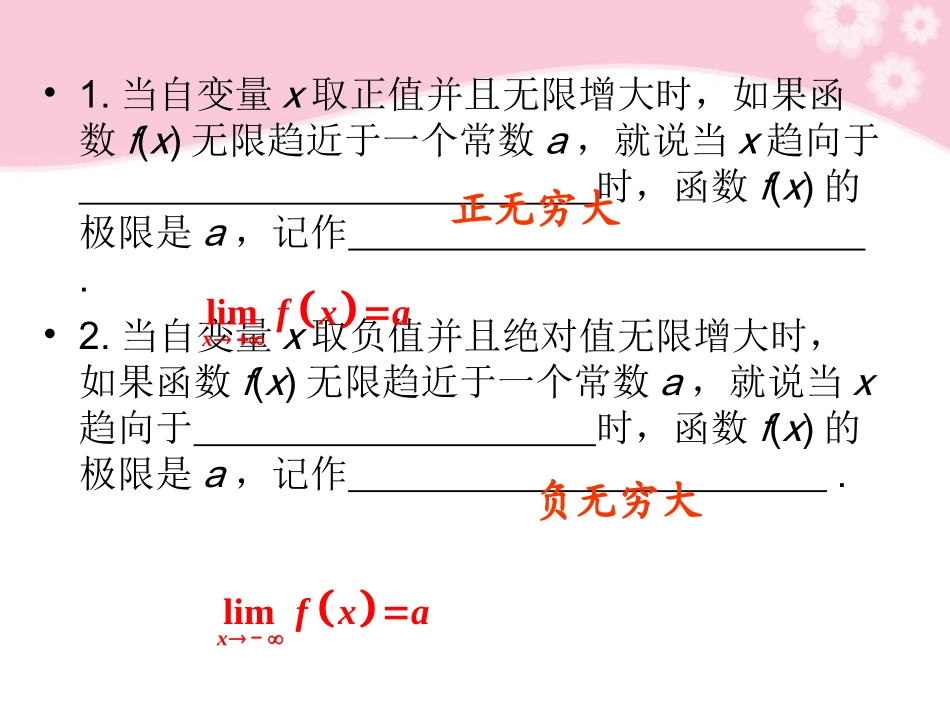
第十二章极限与导数第讲考点搜索●函数极限的有关概念及其符号表示和相互关系●函数极限的四则运算法则●函数的连续性概念，连续函数的图象特征及最大值和最小值定理高高考猜想1.求函数的极限.2.已知函数的极限求相关参数的值.3.函数的连续性分析与讨论.•1.当自变量x取正值并且无限增大时，如果函数f(x)无限趋近于一个常数a，就说当x趋向于时，函数f(x)的极限是a，记作.•2.当自变量x取负值并且绝对值无限增大时，如果函数f(x)无限趋近于一个常数a，就说当x趋向于时，函数f(x)的极限是a，记作.正无穷大负无穷大limxfxalimxfxa－•3.如果且，那么就说当x趋向于时，函数f(x)的极限是a，记作.•4.当自变量x无限趋近于常数x0(但不等于x0)时，如果函数f(x)无限趋近于一个常数a，就说当x时，函数f(x)的极限是a，记作.无穷大趋近于x0limxfxalimxfxalimxfxa0limxxfxa•5.如果当x从点x=x0左侧(即x＜x0)无限趋近于x0时，函数f(x)无限趋近于常数a，就说a是函数f(x)在点x0处的，记作.•6.如果当x从点x=x0右侧(即x＞x0)无限趋近于x0时，函数f(x)无限趋近于常数a，就说a是函数f(x)在点x0处的，记作.•7.的充要条件•是.左极限右极限0limxxfxa0limxxfxa＋0limxxfxa00limlimxxxxfxfxa•8.如果那么•=;•=;•=(b≠0).a±ba·b00limlimxxxxfxagxb，，0lim()()xxfxgx［］0lim()()xxfxgx［］0lim()xxfxgxab•9.如果函数y=f(x)在点x=x0处及其附近有定义，且，就说函数f(x)在点x0处连续.如果函数f(x)在某个区间内都连续，就说函数f(x)在这个区间内连续.•10.如果f(x)是闭区间［a，b］上的连续函数，那么f(x)在闭区间［a，b］上有————————————.最大值和最小值每一点处00limxxfxfx•1.已知函数f(x)是偶函数,且•则下列结论一定正确的是()•解：因为f(x)是偶函数,所以f(-x)=f(x).•又所以•又f(x)=f(-x),所以Blim,xfxaA.limB.limC.limD.lim||xxxxfxafxafxafxalimxfxalim.xfxalimlim.xxfxfxa•2.等于()•解:因为•所以A2212lim45xxxxx121A.B.1C.D.254221222,45155xxxxxxxxxx2211221limlim.4552xxxxxxxx•3.若在点x=0处连续，•则f(0)=.•解:因为f(x)在点x=0处连续，•所以31111xfxx3200lim.xffx300233011limlim11(1)113lim.211xxxxfxxxxx题型1求函数的极限•1.求下列各极限：22024411lim()22lim()cos3lim4lim.||cossin22xxxxxxxaxbxxxxxx；；；•解：(1)原式•(2)原式2224211limlim.424xxxxxlimlim.2111xxabxabxaxbxabababxabxx•(3)因为•所以•所以不存在.•(4)原式00lim1,lim1xxxxxx而，00limlim,||||xxxxxx0lim||xxx2222cossin22limlim(cossin)2.22cossin22xxxxxxxx•点评：若f(x)在x0处连续，则应有•故求f(x)在连续点x0处的极限时，只需求f(x0)即可；若f(x)在x0处不连续，可通过变形，消去因式x-x0，转化成可直接求f(x0)的式子.求分式型函数的极限，一般是先通分、约分，然后再求.若分式中含有根式的，注意分母有理化、分子有理化在变形中的应用.00lim,xxfxfx•求下列极限:(1)•解：(1)原式231321lim;9xxxx3222lim.2121xxxxx23331341lim9(1321)33lim33(1321)31lim.163(1321)xxxxxxxxxxxxxxxx•(2)原式322232222121lim21(21)21lim(21)111lim.11422xxxxxxxxxxxxxxxx...