高中数学 第一章 三角函数 122 同角三角函数课件 新人教A版必修4 课件VIP免费

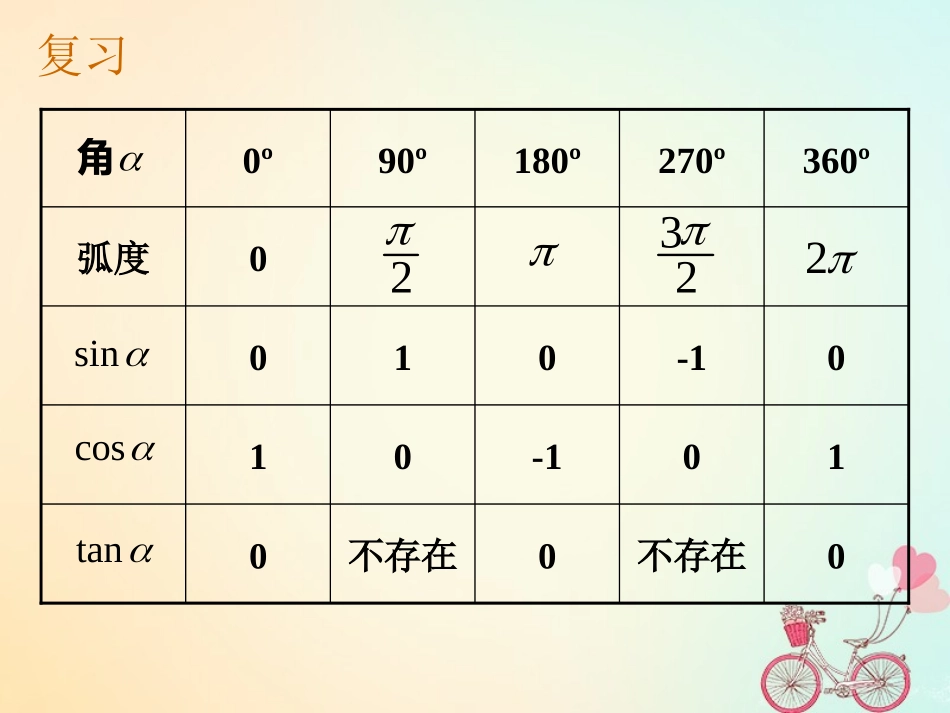
1.2.2同角三角函数的基本关系【目标导学】【主体自学】看书:P21到例6为止1.掌握同角三角函数八个基本关系式2.理解并能熟练运用基本关系式求值0不存在0不存在010-1010-10100弧度360º270º180º90º0º角sincostan2322复习如图，设是一个任意角，它的终边与单位圆交于点P(x,y)，则sinycosxtan(0)yxxxyoP(x,y)1-11-1的终边M22sincos1同角三角函数的基本关系：sintancos(,)2kkZ例1.已知，求的值。3sin5cos,tan解：因为，所以是第三或第四象限角.sin0,sin1且22sincos1由得222162535cos1sin1()若是第三象限角，则，所以cos0416255cos所以353sintan()()cos544若是第四象限角，则43cos,tan54tan3例3.已知，求下列式子的值。23cossin(1);3cossin(2)2sin3sincos.例2.化简。21sin44022sincos1同角三角函数的基本关系：sintan(,)cos2kkZ常用变形：22sin1cos22cos1sinsincostansincostan2221costancos222sintan1sin思考：1sincos,,cossin.842已知且求小结:同角三角函数的八个基本关系式2222221sincos11tansec1cotcsc、平方关系sin2tancoscoscotsin、商数关系3tancot1sincsc1cossec1、倒数关系练习：1.已知，求。5cos13sin,tan2.已知，求。3tan4sin,cos作业P24T5、10、11、123.P23T1~41.2.2同角三角函数的基本关系【目标导学】【主体自学】看书:P22例71.掌握同角三角函数八个基本关系式2.能熟练运用基本关系式证明三角恒等式复习:同角三角函数的八个基本关系式2222221sincos11tansec1cotcsc、平方关系sin2tancoscoscotsin、商数关系3tancot1sincsc1cossec1、倒数关系例1.求证。cos1sin1sincos证明：cos0sin1,1sin0,xxx，由知所以于是cos(1sin)(1sin)(1sin)左边2cos(1sin)1sin2cos(1sin)cos1sincos右边证明等式的常用方法：1.从等式的一边证得它等于另一边；2.先证明另外一个等式成立，从而推出需要证明的等式成立；3.利用作差法。222212sincoscossincossin12sincos例2.求证。练习：求证：442222sincos12sincos(cos1)sin22cos(1)(2)xxxx；思考：1sincos,,cossin.842已知且求练习:P23T5作业P24T9、T13