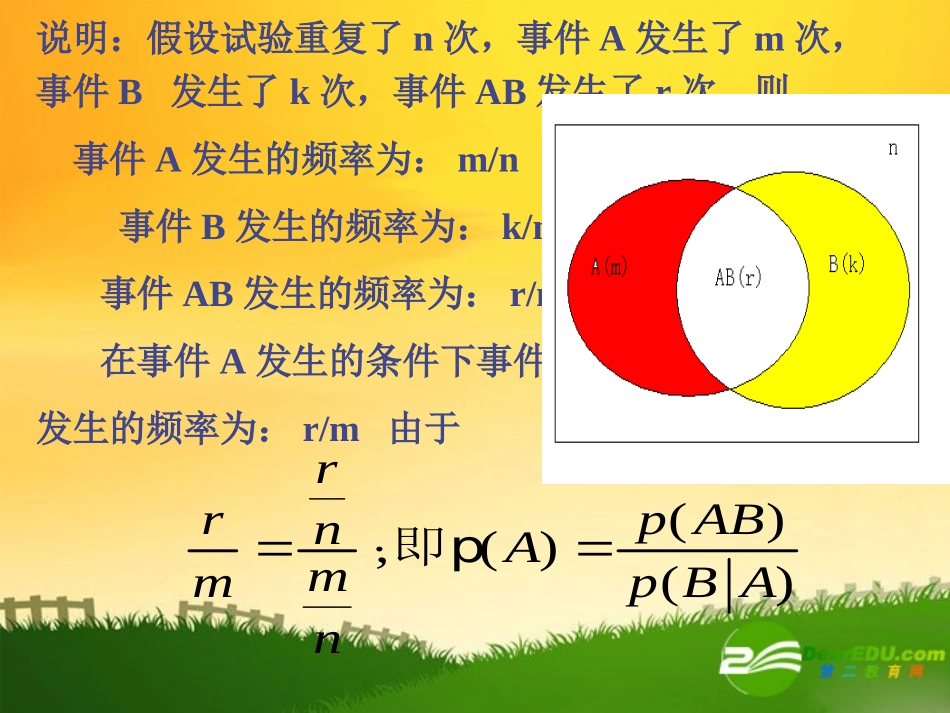
§3条件概率•一、条件概率•二、事件的独立性一、条件概率许多情况下,我们会遇到在事件A发生的条件下求事件B的概率问题,我们把这个概率称为在事件A发生的条件下事件B的条件概率。记作:P(B/A)(课本)定义1:设A、B是样本空间S中的两个事件,且P(A)>0,称)()()(APABPABP为在事件A发生的条件下事件B发生的条件概率。说明:假设试验重复了n次,事件A发生了m次,事件B发生了k次,事件AB发生了r次,则事件A发生的频率为:m/n事件B发生的频率为:k/n事件AB发生的频率为:r/n在事件A发生的条件下事件B发生的频率为:r/m由于B(),()()rrpABnAmmpBAn即p(|)BAPABBABB在发生的条件下包含的样本点数=在发生的条件下样本点数包含的样本点数=包含的样本点数ABPABBPB包含的样本点数/总数()==包含的样本点数/总数()例盒中有球如表.任取一球玻璃木质总计红蓝2347511总计61016若已知取得是蓝球,问该球是玻璃球的概率.变式:若已知取得是玻璃球,求取得是篮球的概率.A:取得是蓝球,B:取得是玻璃球)|(ABP)()(APABP1141611164)|(BAP)()(BPABP64166164解.分别用A、B表示两个随机事件:A={第一次取出的是黑球},B={第二次取出的是黑球};问题转化为计算条件概率P(B|A),根据定义,需要求出概率P(AB)与P(A)。例1.4.1假定盒中装有3个黑球和2个白球,无放回接连取两个小球,已经知道第一次取出的是黑球,问第二次也取出黑球的概率是多少?①交事件AB含义是“从3个黑球和2个白球的5个小球中无放回地接连取出两个,取到的都是黑球”因此P(AB)=C32×C20/C52=0.3;②P(A)有两种不同的解法,依赖于如何构造Ω。解法一:以两次抽样的结果来构造样本空间,需要考虑顺序,因此样本空间的样本点总数是P52=20。根据乘法原理,“第一次取出的是黑球”包含的样本点个数有3×4=12,因此P(A)=12/20=0.6;解法二:以第一次抽样的结果来构造样本空间,从5个小球(包含了3个黑球)中随机取出一个,因此P(A)=3/5=0.6;最后,根据条件概率的定义,有:P(B|A)=0.3/0.6=0.5。□二、事件的独立性•由条件概率我们知道,一般情况下P(B/A)≠P(B),但有时也会出现P(B/A)=P(B)的情况。•例如:同时抛掷两枚均匀的硬币•记A={第一枚出现正面},B={第二枚出现正面}•显然P(B)=1/2,P(B/A)=1/2,也就是说,A事件发生与否不影响事件B发生的概率,即P(B/A)=P(B),这时我们称事件A与B是相互独立的。•在事件A与B相互独立的情况下,乘法公式变得非常简单,即•P(AB)=P(A)P(B)•我们就用上式来定义事件的独立性•定义:设A、B为两事件,若满足P(AB)=P(A)P(B)则称A与B是相互独立的。例:从一幅不含大小王的扑克牌中任抽一张,记A=“抽到K”,B=“抽到黑色的牌”,问事件A与B是否独立?解:P(A)=4/52=1/13,P(B)=26/52=1/2,P(AB)=2/52=1/26,所以P(AB)=P(A)P(B)即A与B是相互独立的。注:实际应用中,对于事件的独立性我们往往不是根据定义来判断,而是根据实际意义来判断。例例1:1:甲、乙、丙三人进行射击,甲击中目标的概率为0.6,乙击中目标的概率为0.55,丙击中目标的概率为0.45。令Ai=“第i人击中目标”,i=1,2,3。(1)求三人都击中目标的概率。(2)求目标被击中的概率。(1)解:P(A1A2A3)=P(A1)P(A2)P(A3)=0.1485第一章小结1.概率论基本概念2.事件间的关系和运算3.概率的基本性质4.古典概型与几何概型5.条件概率、乘法公式及事件的独立性6.全概公式与贝叶斯公式